Нормальное распределение

Определение. Случайная величина Х имеет нормальный закон распределения, если ее функция плотности вероятности имеет вид:

f(x)= ,

где σ и a – параметры распределения.

Определение. График функции f(x) называется нормальной кривой или кривой нормального распределения.

Методами дифференциального исчисления можно установить, что:

1. кривая симметрична относительно прямой х= a;

2. функция имеет максимум при х= a f(a)= ;

3. по мере удаления х от точки a функция убывает и при х→ ∞ кривая приближается к оси Ох;

4. кривая выпукла вверх при х є (a – σ; a + σ) и

выпукла вниз при х є (– ∞; a – σ) и х є (a + σ; + ∞).

f(x)     0 a X

Рис. 4. Кривая нормального распределения.

Свойства нормального распределения.

1. Вероятность того, что нормально распределенная случайная величина Х примет значение, принадлежащее интервалу (α; β), находится по формуле:

Р(α < Х < β) = Ф —Ф ,

где Φ(х) – функция Лапласа (см. приложение 2).

2. Вероятность того, что абсолютная величина отклонения меньше положительного числа δ находится по формуле:

Р( <δ)=2Ф().

В частности при a =0 справедливо равенство: Р( <δ)= 2Ф().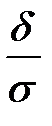

10. функции одного случайного аргумента

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргу-мента Х: Y = φ (X). Выясним, как найти закон распределения функции по известному закону распределения аргумента.

1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Х соот-ветствуют различные значения Y. Тогда вероятности соответствующих значений Х и Y равны.

Date: 2016-07-20; view: 263; Нарушение авторских прав