
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Равномерное распределение
|
|
Формула Бейеса
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) В1, BВ2..., Вn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса где Р(А) = Р (В1) РВ1(А) + Р (В2) РВ2(А) +... + Р (Вn) РВn(А).
4. Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли: 
Вероятность Рn(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m0, а затем уменьшается при изменении m от m0 до n.Поэтому m0, называют наивероятнейшим числом наступлений успеха в опытах. Это число m0, заключено между числами np-q и np+p (или, что то же самое, между числами n(p+1)-1 и n(p+1)).Если число np-q - целое число, то наивероятнейших чисел два: np-q и np+p.
Важное замечание. Если np-q< 0, то наивероятнейшее число выигрышей равно нулю.
5.Локальная теорема Лапласа.
Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р  (k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n):
(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n):
Р  (k) =
(k) = 
где  φ(x) =
φ(x) =  ; q = 1 – p.
; q = 1 – p.
Интегральная теорема Лапласа.
Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P  (k
(k  , k
, k  ) того, что событие А появится в n испытаниях от k
) того, что событие А появится в n испытаниях от k  до k
до k  раз, приближенно равна определенному интегралу:
раз, приближенно равна определенному интегралу:
 ,
,
где 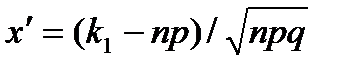 и
и  .
.
Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное дополнение: произведение n∙p сохраняет постоянное значение, а именно, n∙p=λ.
Формула Пуассона имеет вид:
 ,
,
где λ=n∙p.
Эта формула выражает закон Пуассона распределения вероятностей массовых (n велико) и редких (р мало) событий.
6,7. Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными вероятностями. Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, первая строка которой возможные значения xi, а вторая–вероятности pi.
| Х | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
В случае, когда множество значений дискретной случайной величины конечно, сумма вероятностей равна единице:  .
.
Если множество возможных значений случайной величины х бесконечно (счетно), то закон распределения будет иметь следующий вид:
| Х | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
где ряд  сходится и его сумма равна единице:
сходится и его сумма равна единице: 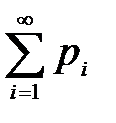 =1.
=1.
Закон распределения дискретной случайной величины х может быть также задан аналитически P(Х= 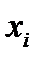 )=j(
)=j( )или с помощью функции распределения.Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки M1(x1;p1), M2(x2;p2), …, Mn(xn;pn) (xi – возможные значения, pi – соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
)или с помощью функции распределения.Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки M1(x1;p1), M2(x2;p2), …, Mn(xn;pn) (xi – возможные значения, pi – соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Математическим ожиданием дискретной случайной величины М(Х) называется число, равное сумме произведений значений случайной величины на соответствующие вероятности их появления:М(Х) = x1 ∙ p1 + x1 ∙ p1 + … + xn ∙ pn
Математическое ожидание обладает следующимисвойствами:
1. Математическое ожидание постоянной величины равно самой постоянной: М(С) = С.
2. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых (то же относится к разности): М(Х ± У) = М(Х) ± М(У).
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий М(Х∙У)=M(Х) ∙ M(У).
4. Постоянный множитель можно выносить за знак математического ожидания: М(С∙Х)=С∙М(Х).
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:D(Х)=M[Х–M(Х)]².
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: D(Х)=M(Х²)–[M(Х)]².
Доказательство. Математическое ожидание М(Х) есть постоянная величина, следовательно, 2∙М(Х) и М²(Х) есть также постоянные величины. Приняв это во внимание и пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии:
D(X) = M[X–M(X)]² = M[X² – 2∙X∙M(X)+M²(X)] = M(X²)–2∙M(X)∙M(X)+M²(X) =
=M(X²) – 2M²(X) + M²(X) = M(X²) – M²(X).
Итак,
D(X) = M(X²) – [M(X)]².
Квадратная скобка введена в запись формулы для удобства ее запоминания.
Свойства дисперсии:
1. Дисперсия постоянной равна нулю: D(C) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D(C∙X)=C² ∙ D(X).
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:иD(X + Y) = D(X) + D(Y).
4. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины: D(X + С) = D(X).
8. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Для непрерывной случайной величины вводится понятие функции распределения. Функцией распределения вероятностей случайной величины Хназывают функцию F(х), определяющую для каждого значения x вероятность того, что случайная величина Х примет значение меньшее x, то естьF(х) = P(X < x)
Часто вместо термина «функция распределения» используют термин «интегральная функция распределения».
Свойства функции распределения:
1. Значения функции распределения принадлежат отрезку [0; 1]:0 ≤ F(х) ≤ 1.
2. Функция распределения есть неубывающая функция, то есть если x  > x
> x  , то F(x
, то F(x  ) ≥ F(x
) ≥ F(x  ).
).
3. Вероятность того, что случайная величина примет значение, заключенное в интервале [a; b), равна приращению функции распределения на этом интервале: P(a ≤ X < b) = F(b) – F(a).
4. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю: Р(Х = x  )=0.
)=0.
5. Если возможные значения случайной величины принадлежат интервалу (а; b), то
F(x) = 0 при х ≤ a;
F(х) = 1 при х ≥ b.
6. Если возможные значения непрерывной случайной величины расположены на всей оси Ox, то справедливы следующие предельные соотношения:
 .
.
Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f(x) = F'(x).
Часто вместо термина «плотность распределения вероятностей» используют термин «плотность вероятностей» и «дифференциальная функция».
Свойства плотности распределения:
1. Плотность распределения неотрицательна в любой точке оси Ох:
f(x)≥0 при х  (– ∞; +∞).
(– ∞; +∞).
2. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, b), определяется равенством:
P(a < X < b) =  .
.
3. Зная плотность распределения, можно найти функцию распределения:
F(x)=  .
.
4. Несобственный интеграл от плотности распределения в пределах от –∞ до +∞ равен единице:
 dx = 1.
dx = 1.
5. Если все возможные значения случайной величины принадлежат интервалу (a; b), то
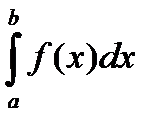 = 1.
= 1.
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством
М(Х)=  ,
,
где f(x) – плотность распределения случайной величины Х.
Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (a; b), то
М(Х)=  .
.
Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной:
М(С)=С.
2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
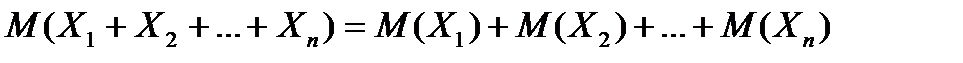 .
.
3. Постоянный множитель можно выносить за знак математического ожидания:
 .
.
4. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
 .
.
Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством:
D(x)= 

Как и в случае с дискретной случайной величиной, можно показать, что
D(x)= 
В частности, если все возможные значения Х принадлежат интервалу (a; b), то
D(X)= 
или
D(X)=  .
.
Дисперсия обладает следующими свойствами:
1. Дисперсия постоянной равна нулю: D(C) =0.
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
D(CХ)=C  D(Х).
D(Х).
3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:
 .
.
4. Дисперсия произведения независимых случайных величин равна произведению дисперсий сомножителей:  .
.
5. Дисперсия суммы постоянной и независимой случайной величины равна квадрату постоянной на дисперсию независимой случайной величины:  .
.
Равномерное распределение
Определение. Будем говорить, что распределение вероятностей непрерывной случайной величины является равномерным распределением, если плотность вероятности случайной величины Х имеет вид:
f(x)= 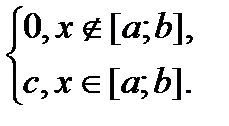
Найдем значение с.
Так как плотность вероятности удовлетворяет условию:  =1,
=1,
то получаем: 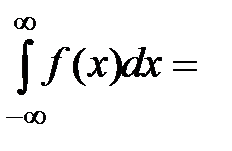
 .
.
Так как f(x)=c на промежутке [a;b], то 

 , следовательно, c =
, следовательно, c =  .
.
Итак, равномерно распределённая случайная величина имеет плотность вероятности:
f(x)= 
Пример. Если распределение случайной величины Х – равномерное и задан отрезок [2;8], то b – a = 8 – 2 = 6 и
f(x)= 
Найдем числовые характеристики равномерного распределения.
1. Математическое ожидание равномерного распределения.
М(Х)=  =
= 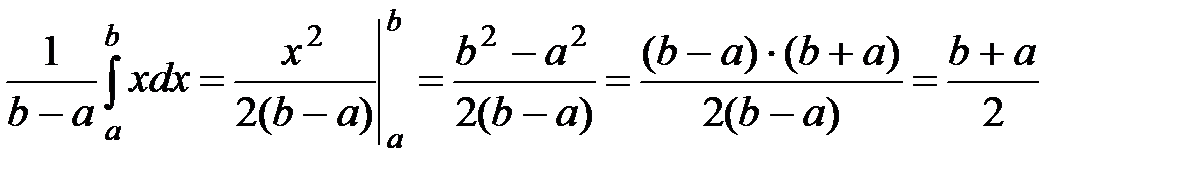 .
.
Пример. Для предыдущей задачи найдем математическое ожидание М(Х)=  .
.
2. Дисперсия равномерного распределения.
D(Х) =  =
=

= 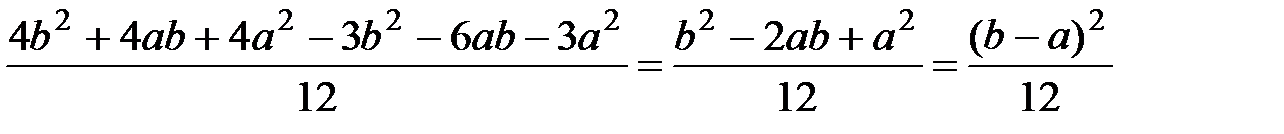 .
.
Date: 2016-07-20; view: 375; Нарушение авторских прав