Определение полинома Жегалкина

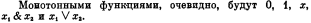
Ксассом линейных функций L назовём множество всех булевых функций, преставление которых в виде полинома Жегалкина не содержит конъюнкций более чем из одной переменной.Очевидно, полином Жегалкина x Ù y не является линейной функцией,

поэтому класс L не является полным.

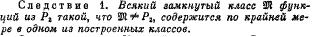
Все они составляют единую предметную область D, а если некоторый квантор должен относиться только к части этой области, то на переменную, по которой он применяется, накладывают ограничение. Ограниченные кванторы не являются новыми логическими операциями; они сводятся к обычным кванторам с помощью следующих определений

Правила общности и, ["(x)A(x)]=и |=A(c) =и "(и),"(л),

[$(x)A(x)] = л |=A(c)=л ($л)

Правила существования ["(x)A(x)]=л|»A(n)=л

[$(x)A(x)]=и|»A(n)=и ($и)

Доказательство. Поскольку система {1 Å,Ù} является полной, и конъюнкция дистрибутивна относительно сложения по модулю 2, то, очевидно, любая булева функция представима в виде полинома Жегалкина. Причем это представление единственно.

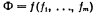
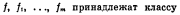
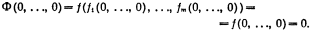
Его замкнутость вытекает из очевидного для самодвойственных функций Тождества Ф*=Ф

Замкнутость L очевидна, т.к.fm = F, где f m- линейные функции, является подстановкой в линейное выражение вместо переменных линейных выражений, из ко- торой после сложения одинаковых констант и переменных может получится только линейный вид полинома Жегалкина

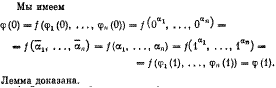
Date: 2016-07-20; view: 447; Нарушение авторских прав