Метод весовых коэффициентов

Успех нахождения компромиссного решения методом весовых коэффициентов целиком зависит от выбора весовых коэффициентов :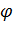

(14.4)

Рассмотрим пример распределения весовых коэффициентов для суточного графика нагрузки электростанции (см. рис. 4.2). Принимая во внимание выше названные критерии — , для провала нагрузки можно сказать, что критерий (экологичность) очень мал, поэтому его весовой коэффициент можно принять минимальным, например, равным = 0,1. Маневренность при провале нагрузки можно и вовсе не учитывать, а весовые коэффициенты по надежности и экономичности принять равными 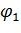= = 0,45.

Недостаток этого метода очевиден:

­ неоптимальный выбор весовых коэффициентов;

­ выполнение итоговой размерности (14.4).

Из-за недостатков данного метода чаще применяют модифицированный метод весовых коэффициентов. Изменения связаны с переходом к безразмерному состоянию:

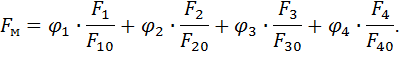
Метод уступок

В рассматриваемом методе изначально выбирается оптимизируемый критерий, например, . Далее решается оптимизационная однокритериальная задача, для фиксированных оставшихся критериев. Решением задачи является вектор матрицы оптимальных значений . После найденного вектора оптимальных решений задается уступка , в пределах которой фиксируется множество решений рис. 14.3.

Рис. 14.3. Найденное оптимальное решение по критерию и указание уступки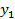

Теперь рассматривается критерий :

Аналогично вышесказанному находят вектор оптимальных значений и выбирают уступку .

Соответствующим образом рассчитывают вектора и .

После рассмотрения всех критериев выбираются два-три варианта из которых наилучший выбирает лицо принимающее решения с уточнением всех возможно неучтенных факторов.

Преимущество данного метода заключается в легком программирование алгоритма вычисления оптимального решения, связанного с решением однокритериальной задачи.

Недостаток метода связан с выбором последовательности расчета. Существуют следующие варианты выбора:

­ по степени важности;

­ применение итерационного метода, связанного с изменением места критерия при его расчете.

Метод ограничений

Рассматриваемые критерии упорядочиваются по степени важности. Для расчетов выбирается самый приоритетный, а остальные критерии вводятся в допустимый диапазон изменений:

Недостаток такого метода связан с громоздкими расчетами.

Date: 2016-07-20; view: 985; Нарушение авторских прав