
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 16. Имитационное моделирование. Основные этапы метода имитационного моделирования. Общая постановка задачи имитационного моделирования.
|
|
Основными этапами метода имитационного моделирования являются:
1. Определение параметров, характеризующих каждое состояние в поведении системы, т.е. определение вектора состояния.
2. Декомпозиция (разбиение) системы на более простые части - блоки. В один блок объединяются "родственные", т.е. преобразующиеся по близким правилам, компоненты вектора состояния и процессы, их преобразующие.
3. Формулируются правила и "правдоподобные" гипотезы относительно поведения системы в целом и ее отдельных частей. В каждом блоке может использоваться свой математический аппарат. Именно это, т.е. блочный способ (принцип), дает возможность установить необходимые пропорции между точностью описания каждого блока, обеспеченностью его информацией и необходимостью достижения цели моделирования.
4. Вводится так называемое системное время, которое моделирует ход времени в реальной системе.
5. Формализованным образом задаются необходимые феноменологические свойства систем в целом и отдельных ее частей.
6. Случайным параметрам, фигурирующим в модели, сопоставляются некоторые их реализации, сохраняющиеся в течение одного или нескольких тактов системного времени. Далее отыскиваются новые реализации.
Общая постановка задачи имитационного моделирования. Под имитационным моделированием обычно понимают пошаговое моделирование поведения объекта с помощью ЭВМ. Это означает, что фиксируются определенные моменты времени t1,t2,...,tn, и состояние модели определяется последовательно в каждом из этих моментов времени. Для реализации этого необходимо задать правило (алгоритм) перехода модели из одного состояния в следующее, т.е. преобразование:  =
=  (
(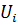 ,
,  ), где
), где  - состояние модели в i-й момент времени.
- состояние модели в i-й момент времени.
Пусть, как обычно, состояние модели определяется вектором:  =(s1,s2,…,sm), т.е. m –числами;
=(s1,s2,…,sm), т.е. m –числами;
состояние среды вектором:Yi = (y1,y2,…,yn), т.е. n - числами,
а состояние управления вектором: 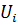 = (
= ( ,
, 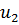 ,…,
,…, 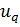 ), т.е. q - числами.
), т.е. q - числами.
Тогда имитационная модель определяется оператором F, с помощью которого можно определить состояние модели в последующий момент времени, т.е. определить вектор  , зная состояние модели в предыдущий момент времени
, зная состояние модели в предыдущий момент времени  и значения Yi и
и значения Yi и 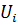 , т.е.
, т.е.  = F(
= F( , Yi,
, Yi, 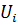 )
)
Таким образом, состояние в имитационной модели определяется рекуррентно на каждом шаге, исходя только из предыдущего шага.
где F - оператор имитаций изменения состояния модели. Он и определяет имитационную модель объекта.
Имитационное моделирование позволяет учитывать неконтролируемые факторы Е объекта, т.е. его стохастичность, в этом случае модель можно представить рекуррентным соотношением вида:
 = F(
= F( , Yi,
, Yi, 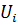 ,
, 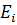 )
)
где необходимо знать, каким образом фактор Е влияет на состояние S объекта. Для работы с такой моделью необходимо знать конкретные значения фактора E, для реализации которого используется метод Монте-Карло.
Для реализации метода Монте-Карло необходимо знать некоторые статистические свойства фактора Е (например, закон его распределения). Эти свойства, вообще говоря, могут зависеть от Y, X и U. Располагая этими сведениями, можно моделировать фактор E в виде случайных рядов:
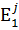 ,
, 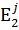 ,…,
,…, 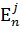 , j = 1, 2,..., n,
, j = 1, 2,..., n,
где индекс внизу соответствует дискретному времени, а верхний ‑ номеру моделируемого ряда (всего моделируется n таких статистически эквивалентных рядов). Естественно, ни один из этих рядов не является точной реализацией действительности, но каждый имеет такие же статистические свойства, что и реальный. Именно поэтому ряды  , позволяют исследовать статистические свойства модели.
, позволяют исследовать статистические свойства модели.
Таким образом, поведение модели " в среднем" описывается как:
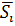 =
= 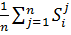 i =1,2,…n, где
i =1,2,…n, где
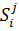 = F(
= F( , Yi,
, Yi, 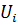 ,
, 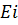 )
)
j-я реализация поведения модели в i-ый момент времени:
Дисперсия выхода модели вычисляется по формуле:
D( ) =
) = 
Таким образом, метод Монте-Карло позволяет оценить статистические свойства поведения объекта путем вероятностного "разыгрывания" поведения модели, причем одна реализация поведения отличается от другой различными значениями фактора Е.
В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета.
Тема 17. Эвристические методы принятия решений. Эвристические деревья решений. Табличное представление инженерных знаний. Формализация представления инженерных решений в форме информационных таблиц.
Ускоренный прогресс в методах сбора, хранения и обработки данных позволил организациям собирать огромные массивы данных, для анализа которых возможностей экспертов уже не хватает. Поэтому спрос на методы автоматического исследования (анализа) данных с каждым годом постоянно увеличивается.
Деревья решений – один из таких методов автоматического анализа данных, представляющий собой способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение. Под правилом понимается логическая конструкция, представленная в виде "если... то..." (рис. 2.14)
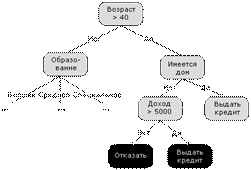 Деревья решений являются удобным инструментом в системах поддержки принятия решений, интеллектуального анализа данных (datamining). В состав многих пакетов, предназначенных для интеллектуального анализа данных, уже включены методы построения деревьев решений. В областях, где высока цена ошибки, они послужат отличным подспорьем аналитика или руководителя.
Деревья решений являются удобным инструментом в системах поддержки принятия решений, интеллектуального анализа данных (datamining). В состав многих пакетов, предназначенных для интеллектуального анализа данных, уже включены методы построения деревьев решений. В областях, где высока цена ошибки, они послужат отличным подспорьем аналитика или руководителя.
Рис. 2.14. Пример дерева решений
Деревья решений имеют ряд преимуществ:
· быстрый процесс обучения;
· генерация правил в областях, где эксперту трудно формализовать свои знания;
· извлечение правил на естественном языке;
· интуитивно понятная классификационная модель;
· высокая точность прогноза, сопоставимая с другими методами (статистика, нейронные сети);
· построение непараметрических моделей.
Конечно, пример дерева решений (рис. 2.14) служит лишь для иллюстрации метода и не пригоден для использования в программных реализациях.
Традиционным и наиболее распространённым способом представления инженерных знаний, содержащихся в справочниках или иных методических материалах, являются информационные таблицы, которые можно условно разделить на несколько категорий.
Справочными таблицами без условий называют таблицы, в которых перечислены наименования и рекомендуемые значения некоторых характеристик какого-либо объекта без каких либо дополнительных условий.
Справочной таблицей с условиями называется упорядоченная совокупность выбираемых значений, каждому из которых поставлены в соответствие одно или два набора условий. По своей семантике выбираемые значения обычно являются качественными и/или количественными значениями определённой характеристики объекта из некоторой предметной области. Выбираемым значением может служить одно слово или последовательность слов. Выбираемые значения могут быть упорядочены в виде последовательности или в виде таблицы.
Рассмотрим процесс формализации представления инженерных знаний в табличной форме:
Действие первое - создаётся таблица из двух строк и числом столбцов, равным числу выделенных абзацев. Выполняется операция объединения ячеек первой строки и в эту строку помещается общая группа подлежащего, а во вторую по соответствующим ячейкам - остальной текст.
| 1.Коэффициент защиты | |||
| 1.1. сетей, для которых защита от перегрузки обязательна, для проводников с резиновой и аналогичной по тепловым характеристикам изоляцией во взрыво- и пожароопасных производственных, служебных, служебно-бытовых помещениях, независимо от рода проводника (осветительные сети), для токов защиты: Iном_вст и Iуст_е_о равен 1.25; а для Iсраб_комб_нр иIсраб_теп_рег равен 1. | 1.2. сетей, для которых защита от перегрузки обязательна, для проводников с резиновой и аналогичной по тепловым характеристикам изоляцией во невзрыво- и непожароопасные помещения (например, провода АПР, ПР на роликах и изоляторах) для токов защиты:Iном_вст, Iуст_е_о, Iсраб_комб_нр иIсраб_теп_рег равен 1. | 1.3. сетей, для которых защита от перегрузки обязательна, дляпроводников с бумажной изоляцией и изоляцией из вулканизированного полиэтилена для токов защиты: Iном_вст, Iуст_е_о, Iсраб_комб_нр равен 1, аIсраб_теп_рег равен 0.8. | 1.4. сетей, не требующих защиты от перегрузки (требуется только защита от токов КЗ), для токов защиты: Iном_вст равен 0.33; Iуст_е_о равен 0.22; Iсраб_комб_нр равен 1 иIсраб_теп_рег равен 0.8. |
Действие второе - ячейки второй строки, начинающиеся одинаковой фразой, разбиваются каждая на две и ячейки второго уровня и объединяются. В объединённую ячейку помещается общая фраза.
| 1. Коэффициент защиты | |||
| 1.1. сетей, для которых защита от перегрузки обязательна | 1.2. сетей, не требующих защиты от перегрузки (требуется только защита от токов КЗ), для токов защиты: Iном_вст равен 0.33; Iуст_е_о равен 0.22; Iсраб_комб_нр равен 1 иIсраб_теп_рег равен 0.8. | ||
| 1.1.1. для проводников с резиновой и аналогичной по тепловым характеристикам изоляцией во взрыво- и пожароопасных производственных, служебных, служебно-бытовых помещениях), независимо от рода проводника (осветительные сети), для токов защиты: Iном_вст и Iуст_е_о равен 1.25; а для Iсраб_комб_нр иIсраб_теп_рег равен 1. | 1.1.2. для проводников с резиновой и аналогичной по тепловым характеристикам изоляцией в невзрыво- и непожароопасные помещения (например, провода АПР, ПР на роликах и изоляторах) для токов защиты:Iном_вст, Iуст_е_о, Iсраб_комб_нр иIсраб_теп_рег равен 1. | 1.1.3. дляпроводников с бумажной изоляцией и изоляцией из вулканизированного полиэтилена для токов защиты: Iном_вст, Iуст_е_о, Iсраб_комб_нр равен 1, аIсраб_теп_рег равен 0.8. | |
Действие третье - выполняются операции разбиения и объединения первых двух ячеек третьей строки.
| 1. Коэффициент защиты | |||
| 1.1. сетей, для которых защита от перегрузки обязательна | 1.2. сетей, не требующих защиты от перегрузки (требуется только защита от токов КЗ), для токов защиты: Iном_вст равен 0.33; Iуст_е_о равен 0.22; Iсраб_комб_нр равен 1 иIсраб_теп_рег равен 0.8. | ||
| 1.1.1. для проводников с резиновой и аналогичной по тепловым характеристикам изоляцией | 1.1.2. дляпроводников с бумажной изоляцией и изоляцией из вулканизированного полиэтилена для токов защиты: Iном_вст, Iуст_е_о, Iсраб_комб_нр равен 1, аIсраб_теп_рег равен 0.8. | ||
| 1.1.1.1. во взрыво- и пожароопасных производственных, служебных, служебно-бытовых помещениях, независимо от рода проводника (осветительные сети), для токов защиты: Iном_вст и Iуст_е_о равен 1.25; а для Iсраб_комб_нр иIсраб_теп_рег равен 1. | 1.1.1.2. в невзрыво- и непожароопасные помещениях (например, провода АПР, ПР на роликах и изоляторах) для токов защиты:Iном_вст, Iуст_е_о, Iсраб_комб_нр иIсраб_теп_рег равен 1. | ||
В результате проведённых формальных действий получена не полностью оптимизированная иерархическая кросс-таблица, сохранившая грамматическую структуру исходного текста, но более удобная в употреблении в силу своей наглядности.
Date: 2016-07-20; view: 590; Нарушение авторских прав