Тема 15. Сетевые методы принятия решений. Алгоритм выбора самого дешёвого пути. Задача о максимальном потоке. Сетевые графики.

Алгоритм выбора самого дешёвого пути. Пусть дана ненаправленная сеть с M вершинами и N рёбрами. Каждому ребру (i,j) поставлена в соответствие цена c(i,j). Каждой вершине i приписываются два текущих (переменных) значения P(i) и K(i), которые будут меняться в процессе реализации алгоритма. P*(i) – это предшествующая вершина вершине i на самом дешёвом пути, а окончательное постоянное значение K*(i) – цена самого дешёвого пути от начала до вершины i.

Прямой поиск.

Шаг 1.

1.1. Отметить начальную вершину P=0, K=0.

1.2. Присвоить постоянные значения P*=0, K*=0

1.3. Присвоить всем остальным вершинам значения P(i)=0 и K(i) = 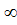(число > max(c(i,j))

Шаг 2.

1.1. Для всех рёбер, соединяющих текущую вершину i с другими непомеченными вершинами j, вычислить сумму K(i)+c(i,j), и если она меньше текущего значения K(j) принять её в качестве нового значения K(j), а в качестве P(j) принять значение I; в противном случае значения K(j) иP(j) не менять.

1.2. Непомеченную вершину с наименьшим значением K(j) пометить путём объявления значений P*(j) и K*(j) постоянными.

Шаги 3,4… Шаг 2 повторяется до тех пор, пока все вершины не окажутся отмеченными в качестве постоянных. В этом случае значения K(i) для каждой вершины будет являться ценой самого дешёвого пути из начальной вершины в вершину i.

Обратный поиск.

Шаг 1. Для каждой вершины i (за исключением начальной) ребро P*(i), т.е. ребро соединяющее предшествующую вершину с вершиной i отмечается специальным образом и объявляется критическим. Множество критических рёбер образует дерево наиболее дешёвых путей для начальной вершины.

Шаг 2. Для определения наиболее дешёвого пути от начала к любой вершине i осуществляется обратный поиск от i к предшествующей её вершине P*(i) и т.д., пока не будет достигнута начальная вершина.

Примечание. Алгоритм наиболее дешёвого пути решает задачу оптимизации с дискретными переменными без применения дифференциального исчисления. Задачу о самом дешёвом пути можно сформулировать и в терминах динамического программирования.

Задача о максимальном потоке. В сетях с ограниченной пропускной способностью, т.е. рёбра имеют вполне определённые пропускные способности, важной является задача об определении максимально возможного потока из одной вершины в другую. Теорема о макси-потоке на мини-сечении утверждает, что максимальный поток от одной вершины сети с ограниченной пропускной способностью к другой равен минимуму пропускных способностей сечений, разделяющих эти вершины.

Сетевые графики. В планировании и управлении различными экономическими объектами часто применяются сетевые методы или, как их иначе называют, сетевые графики. Для построения сетевого графика, прежде всего, определяется список всех работ или действий требуемых для выполнения процесса.

Затем оценивается продолжительность или время, необходимое на завершение работы и определяются зависимости между операциями, т.е. какие работы должны быть закончены, прежде чем начнутся другие.

Результаты работ (события) будем изображать кружком с соответствующим номером внутри. При этом, если работа i предшествует работе j, то будем изображать так:

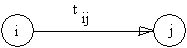
Пусть далее t_ij означает, что работа j может быть завершена через время t_ij после окончания работы i. Будем считать, что величины t_ij для всего списка работ известны. Стрелка на этой модели обозначает собственно работу, а кружки - результат.

Эту простую схему применим для всего спектра работ. В результате получим следующую схему, изображенную в виде графика (рис.1.1):

Рис. 1.4. Пример сетевого графика.

Сетевая модель, отображающая процесс выполнения комплекса работ, направленных на достижение единой цели, может быть изображена либо в виде сетевого графика (рис.1.4).

Date: 2016-07-20; view: 458; Нарушение авторских прав