Точечные оценки параметров

Важной задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака X генеральной совокупности. Другими словами, необходимо по данным выборочного распределения оценить неизвестные параметры теоретического распределения. Статистические оценки могут быть точечными и интервальными.

Статистикой называется любая функция выборочных значений x₁, x₂,... x_n: G = G(x₁, x₂,... x_n). Точечной оценкой неизвестного параметра называют число (точку на числовой оси), которое приблизительно равно оцениваемому параметру и может заменить его с достаточной степенью точности в статистических расчетах.

Точечной оценкой генеральной средней 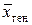и параметра a может служить выборочная средняя .

Точечными оценками генеральной дисперсии могут служить выборочная дисперсия , или, при малых объемах выборки n, исправленная выборочная дисперсия: .

Точечными оценками для генерального среднеквадратического отклонения могут служить: – выборочное среднее квадратическое отклонение или – исправленное выборочное среднее квадратическое отклонение.

Формулы, необходимые для вычисления выборочной средней и выборочной дисперсии , приведены в п. 2.

Для того чтобы точечные статистические оценки обеспечивали “хорошие” приближения неизвестных параметров, они должны быть несмещенным и, состоятельными и эффективными.

Пусть – точечная оценка неизвестного параметра q.

Несмещенной называют такую точечную статистическую оценку , математическое ожидание которой равно оцениваемому параметру: .

Состоятельной называют такую точечную статистическую оценку, которая при стремится по вероятности к оцениваемому параметру. В частности, если дисперсия несмещенной оценки при стремится к нулю, то такая оценка оказывается и состоятельной.

Эффективной называют такую точечную статистическую оценку, которая при фиксированном n имеет наименьшую дисперсию.

Можно показать, что выборочная средняя является несмещенной, состоятельной и эффективной оценкой генеральной средней .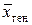

Для построения интервальной оценки рассмотрим событие, заключающееся в том, что отклонение точечной оценки параметра от истинного значения этого параметра q по абсолютной величине не превышает некоторую положительную величину D. Вероятность такого события . Заменив неравенство на равносильное, получим: .

Вероятность того, что доверительный интервал заключает в себе (покрывает) неизвестный параметр q равна g и называется доверительной вероятностью или надежностью интервальной оценки. Величину D называют точностью оценки.

Построим интервальную оценку параметра для двух случаев:

1) параметр s нормального закона распределения признака Х генеральной совокупности известен. В этом случае интервальная оценка параметра с заданной надежностью g определяется формулой:

,

где D= , t – аргумент функции Лапласа: Ф (t) = (прил. 2).

2) параметр s нормального закона распределения признака Х генеральной совокупности неизвестен. В этом случае интервальная оценка параметра с заданной надежностью g определяется формулой:

,

где D = 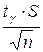, S – точечная оценка параметра s, – значения распределения Стьюдента, которые находим по таблице

Date: 2016-07-18; view: 334; Нарушение авторских прав