Последовательное соединение

Под последовательным соединением элементов в теории надежности понимают такое соединение, при котором отказ одного какого-либо элемента влечет за собой отказ всей системы.

Пример. На рисунке 4.4 приведена схема реактора с герметическим приводом.

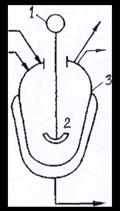
Рисунок 4.4. - Схема реактора с герметическим приводом

Схема надежности реактора будет иметь вид, приведенный
на рисунке 4.5.

Р₁ Р₂ Р₃

Рисунок 4.5. - Схема надежности реактора

При рассмотрении схемы (см. рисунок 4.5) легко видеть, что при отказе любого элемента будет иметь место отказ функционирования всей системы.

Тогда, вероятность безотказной работы реактора равна:

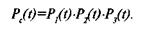(4.1)

Для определения вида соединения необходимо, перечисляя каждый элемент системы друг за другом, задавать вопрос: если этот элемент откажет, то откажет ли вся система? Если система откажет, то данный элемент включен последовательно; если система не откажет, то имеет место другой вид соединения.

На рисунке 4.6 представлены множества Р₁, Р₂, Р₃, представляющие собой функционирование соответствующего элемента по рисунку 4.5, т.е.:

- если вероятность безотказной работы (надежность) привода - это попадание точки в область Р_1;

- вероятность безотказной работы (надежность) перемешивающего устройства - это попадание точки в область Р₂;

- и надежность корпуса – попадание точки в область Р₃,

- то множество работоспособных состояний всей системы Р_с соответствует пересечению множеств Р₁, Р₂, Р₃.

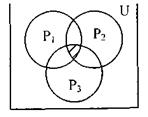
Рисунок 4.6 - Последовательное соединение

Тогда для надежности системы можно записать:

(4.2)

Надежность зависит от времени.

Итак, расчетная формула для определения показателя надежности системы с последовательным соединением элементов:

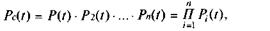(4.3)

Из этой формулы можно сделать следующие выводы:

1) надежность системы с последовательно включенными элементами всегда будет ниже надежности самого ненадежного элемента системы:

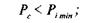
Date: 2016-07-18; view: 311; Нарушение авторских прав