Выбор закона распределения

Гипотеза распределения принимается по следующей методике:

1 Определяем вид выборки
N < 20 - малая выборка	N > 20 - большая выборка
2 Строится вариационный ряд наработки: t1 < t2 < t3 < t4 < … <tn.	2 Общее время наработки до отказа ti разбивается на К интервалов только для большой выборки: ; К – число интервалов на практике К=4-12; Δt – ширина интервала; tmax, tmin - максимальное и минимальное значение показателя
3 Для каждого значения Определяются показатели надежности Pi(t), F(t), li(t). Результаты сводятся в таблицу	3 Для каждого интервала определяются эмпирические характеристики: ni – число отказов в каждом интервале; Р0 – опытная вероятность; li(t) - оценка интенсивности отказов; Pi(t) оценка вероятности безотказной работы в интервале. Результаты сводятся в таблицу
4 Строятся гистограммы Pi(t), F(t), li(t). По виду гистограмм высказывается гипотеза о законе распределения:	4 Строятся гистограммы Pi(t), li(t). По виду гистограмм высказывается гипотеза о законе распределения:
- если l(t) = const, то принимается гипотеза об экспоненциальном законе; - l(t) имеет минимум в середине интервала, то принимается нормальный закон распределения; - если l(t) убывает или возрастает с увеличением t, то имеет место закон Вейбула-Гнеденко
5 Оценка параметров предполагаемого закона распределения
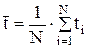- среднее арифметическое значение случайной величины; - коэффициент вариации; - среднее квадратическое отклонение	- среднее арифметическое значение случайной величины; Ро – опытная вероятность i-го интервала; - коэффициент вариации; - среднее квадратическое отклонение
6 Проверка гипотезы о предполагаемом законе распределения:
по критерию Колмогорова	по критерию Пирсона
Dmax=F*(t) - F(t), где F*(t) – статистическая функция; F(t) – теоретическая функция; - условная интенсивность. Если Р(l) ³ 0,5, то гипотеза не противоречит опытным данным.	Если , то гипотеза подтверждается. χ2 - табличное значение (выбирается по Р и r); r = K – S + 1 – число степеней свободы; K – число интервалов; S – число обязательных связей: S =2 для нормального закона; S =1 для экспоненциального закона; S = 3 для закона Вейбула; ni – частота в i-ом интервале.

Date: 2016-07-18; view: 313; Нарушение авторских прав