Общие принципы и методика регрессионного анализа

Согласно принятому определению, регрессионный анализ представляет собой статистический метод анализа и обработки экспериментальных данных, используемый при воздействии на отклик только количественных факторов и основанный на сочетании аппарата МНК и техники статистической проверки гипотез.

Этот метод базируется на рассмотренных ранее основных положениях математической статистики и используется для проверки ряда гипотез, совместное принятие которых позволяет установить факт статистического соответствия (или несоответствия) полученной математической модели исследуемому процессу с любым заданным уровнем значимости.

Регрессионный анализ, как и всякий статистический метод, основан на ряде постулатов, главными из которых являются следующие:

1. Каждый из откликов у_i, полученных при параллельных измерениях, является случайной величиной, нормально распределенной относительно своего центра у_0,i в любой i -ой точке факторного пространства.

2. Дисперсия генеральной совокупности этой случайной величины независима от значений отклика у_i и постоянна во всех точках факторного пространства.

3. Уровни факторов являются детерминированными величинами, то есть такими «не случайными» величинами, которые в процессе эксперимента воспроизводятся и измеряются с абсолютной точностью.

Практически это означает, что ошибка эксперимента, связанная с фиксированием и поддержанием факторов на заданных уровнях, является несоизмеримо меньшей по сравнению с ошибкой измерения откликов. Таким образом, в процессе регрессионного анализа необходимо, прежде всего, проверить гипотезы, связанные с выполнением основных постулатов, и только потом оценить адекватность полученной математической модели.

Проверка первого постулата может быть произведена по методике с использованием критерия согласия Пирсона χ2.

Проверка гипотезы об однородности дисперсий в нескольких выборках.Критерий Кохрена. При статистической обработке массивовэкспериментальных данных часто возникает задача одновременной оценкиоднородности нескольких дисперсий, рассчитанных на основании данныхполученных из разных выборок.В частности, такая задача всегда должна предшествовать рассмотренной выше проверке адекватности математических моделей.

Дело в том, что, согласно одному из основных постулатов регрессионногоанализа, математическое описание процессов может иметь смысл толькопри условии воспроизводимости эксперимента. Это означает, что впределах всей генеральной совокупности исследуемой величины у дисперсия воспроизводимости должна быть постоянной, не зависящейот абсолютных значений y в разных точках факторного пространства. Таким образом, процедура проверки адекватности любыхматематических моделей правомерна только при условии однородностивыборочных дисперсий воспроизводимости, рассчитанных при всех исследованных комбинациях уровней варьирования факторов.

При числе выборок, большем двух, и равномерном дублировании опытов проверку однородности выборочных дисперсий принято производить при помощи G −критерия Кохрена, рассчитываемого по формуле:

где числитель – выборочная дисперсия воспроизводимости, имеющая максимальное значение;

знаменатель − cумма всех сравниваемых дисперсий, включая и максимальную;

N – число выборок (равное числу точек факторного пространства).

G – критерий представляет собой случайную функцию G m1 ,m 2, подчиняющуюся распределению Кохрена, таблицы квантилей которого имеются в специальной литературе. Индексы m 1 и m ₂ означают два характерных числа степеней свободы: m ₁ = (n − 1), то есть число степеней

свободы, с которым определялась максимальная дисперсия, а m ₂ = N, где N - число слагаемых в знаменателе формулы.

Область принятия основной гипотезы в данном случае ограничивается выполнением условия: G < Gтаб.

Однако экспериментаторы редко располагают достаточным объемом параллельных наблюдений, поэтому в большинстве случаев приходится принимать этот постулат на веру без дополнительной проверки.

Проверка справедливости второго постулата является обязательной. Для этого, как правило, используется G -критерий Кохрена. Процедура заключается в проверке гипотезы об однородности выборочных дисперсий в различных точках факторного пространств. Принятие этой гипотезы позволяет считать все построчные дисперсии воспроизводимости (рассчитанные, например, по отдельным строкам табл. 1) случайными выборками из одной и той же генеральной совокупности, что дает право, объединив эти выборки, использовать для расчета общей дисперсии воспроизводимости эксперимента.

Результирующая дисперсия воспроизводимости эксперимента при равномерном дублировании опытов может быть определена по формуле:

Третий постулат не может быть проверен статистическими методами. Однако о нем нужно постоянно помнить как на стадии подготовки, так и на стадии выполнения эксперимента. В частности, при разработке опытных установок следует уделять особое внимание обеспечению возможности точной фиксации дискретных уровней всех варьируемых факторов, используя для этого специальные конструктивные приемы и применяя высокоточные средства для измерения этих фиксируемых уровней.

Описанные процедуры считаются вспомогательными и должны обязательно предшествовать основным. Основными же процедурами регрессионного анализа являются: оценка значимости коэффициентов регрессии и проверка гипотезы об адекватности полученной математической модели.

Для статистической оценки значимости коэффициентов по результатам эксперимента предварительно вычисляются оценки дисперсий и СКО каждого u −го коэффициента регрессии: и .

При использовании в математической модели натуральных (то есть не нормализованных) значений всех факторов расчет оценок дисперсии и СКО коэффициентов регрессии может быть выполнен по формулам:

где – оценка так называемой «дисперсии среднего», вычисляемая по результатам всего эксперимента как:

где - средневзвешенная дисперсия воспроизводимости, рассчитанная для объединенной выборки, содержащей данные всего эксперимента;

n – число равномерно дублируемых параллельных опытов.

Далее с использованием t − критерия Стьюдента определяются доверительные интервалы каждого коэффициента регрессии

где t _{α ,m} - табличное значение критерия Стьюдента при заданном уровне значимости α и числе степеней свободы m = N(n – 1 ), с которым определялась дисперсия воспроизводимости.

Значимыми считаются те коэффициенты, абсолютная величина которых больше доверительного интервала:

Проверка значимости коэффициентов приобретает особый смысл при обработке результатов многофакторного эксперимента. Наличие незначимого коэффициента в аппроксимирующем уравнении при одном из факторов свидетельствует о том, что, выполнив эксперимент с данной степенью точности, нельзя однозначно ответить на вопрос о влиянии данного фактора на исследуемую функцию. Другими словами: cуществование зависимости между исследуемой функцией и параметром, при котором имеется незначимый коэффициент, статистически не подтверждается.

Поэтому, признав коэффициент незначимым, следует исключить соответствующий фактор х_u из полученного уравнения регрессии, добавив одновременно к свободному члену постоянную величину, определяемую как произведение среднего значения этого фактора во всем исследованном диапазоне на незначимый коэффициент .

Если же неравенство выполняется, то наличие зависимости между величинами х и у следует считать статистически подтвержденным фактом, после чего следует перейти к оценке адекватности математической модели.

Адекватными принято считать такие математические модели, при использовании которых для описания экспериментальных зависимостей соблюдается условие однородности двух дисперсий: дисперсии воспроизводимости и дисперсии адекватности .

При этом общая дисперсия воспроизводимости эксперимента в случае однородности всех построчных дисперсий рассчитывается как средневзвешенная величина.

Дисперсия адекватности математической модели рассчитывается по формуле:

где L – количество значимых коэффициентов в уравнении регрессии;

– среднеарифметические экспериментальные значения отклика, полученные при каждом i – м уровне фактора;

– расчетные значения отклика, определяемые при помощи выбранной математической модели;

N – число точек факторного пространства, в которых ставились опыты;

n – количество параллельных опытов в каждой i − й точке.

После вычисления значений двух указанных дисперсий, проверка их однородности может быть осуществлена с использованием F − критерия Фишера. В случае подтверждения однородности этих дисперсий математическая модель признается адекватной.

Проверка гипотезы об однородности дисперсий. Критерий Фишера.

Математические модели могут быть аналитическими или эмпирическими. В первом случае они представляют собой строгие аналитические решения, полученные на основе известных физических законов и соотношений, а во втором – зависимости, полученные в результате аппроксимирования результатов эксперимента.

Как в том, так и в другом случае при сопоставлении экспериментальных точек с расчетными кривыми всегда имеют место две дисперсии: дисперсия воспроизводимости и дисперсия адекватности .

Первая из этих дисперсий характеризует разброс результатов параллельных наблюдений относительно среднеарифметических значений, вычисленных по этим результатам на каждом дискретном уровне (или при каждом возможном сочетании дискретных уровней разных факторов в многофакторном эксперименте). Вторая дисперсия количественно характеризует разброс полученных среднеарифметических значений относительно аналитической или аппроксимирующей кривой.

Вывод об однородности дисперсий воспроизводимости и адекватности всегда имеет принципиальный характер, так как позволяет отнести обе дисперсии к одной и той же генеральной совокупности. А это, в свою очередь, статистически подтверждает адекватность предлагаемой

математической модели, свидетельствуя о том, что выбранная аналитическая (или аппроксимирующая) функция не противоречит опытным данным в пределах точности поставленного эксперимента.

Рассмотрим общий порядок проверки статистической гипотезы об однородности двух выборочных дисперсий. Пусть для двух независимых выборок (объемами N ₁ и N ₂) из нормальной генеральной совокупности получены оценки и . Требуется проверить нулевую гипотезу Но,

заключающуюся в том, что σ₁ = σ₂, относительно альтернативной гипотезы Н 1, которая заключается в том, что σ₁ > σ ₂.

В качестве критерия для проверки нулевой гипотезы в данном случае принято использовать отношение большей из двух выборочных дисперсий – к меньшей - , то есть случайную функцию , имеющую распределение Фишера со степенями свободы m ₁ и m ₂, которая получила название критерия Фишера. Символом m ₁ принято обозначать число степеней свободы, при котором вычисляется значение большей выборочной дисперсии, а символом m ₂ – меньшей.

Процедура проверки нулевой гипотезы Ho состоит в том, что по экспериментальным данным вычисляется фактическое значение F −критерия Фишера, которое сравнивается с табличным значением − Fтаб, определенным при выбранном уровне значимости* α и соответствующих степенях свободы m ₁ и m ₂. Область принятия гипотезы ограничивается условием F < Fтаб, при выполнении которого нулевая гипотеза принимается c заданным уровнем значимости.

Пример. Оценим значимость коэффициентов и адекватность линейной однофакторной математической модели (10), полученной ранее в результате аппроксимирования данных табл. 1. Вспомогательные параметры для расчета дисперсий воспроизводимости и адекватности, вычисленные на основе данных табл. 1, представлены в табл. 2.

Таблица 2

Параметры для расчета дисперсий

в рассматриваемом примере

Построчные дисперсии в каждой i –й строке этой таблицы рассчитаны по формуле:

Эти дисперсии характеризуют разброс экспериментальных значений, полученных в каждом опыте. Для проверки гипотезы об однородности построчных дисперсий вычислим фактическое значение G -критерия Кохрена по формуле:

Табличное значение этого критерия Gтаб = 0,561 (при числе степеней свободы m ₁ = n – 1 = 2; m 2 = N = 7 и уровне значимости α = 0,05). Так как фактическое значение G −критерия не превышает табличного, гипотеза об однородности построчных дисперсий принимается. Это дает право объединить построчные выборки и вычислить общую дисперсию воспроизводимости эксперимента:

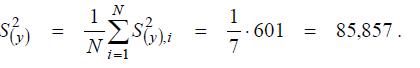
Далее вычислим три следующих параметра: «дисперсию среднего»; оценку дисперсии коэффициента уравнения регрессии k; СКО коэффициента регрессии:

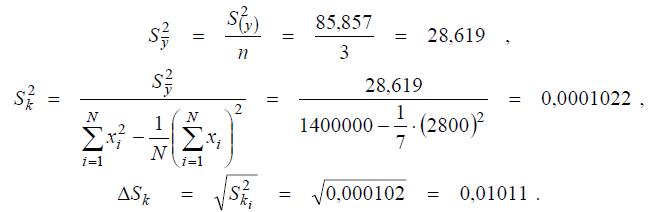
Для расчета доверительного интервала необходимо определить табличное значение t −критерия Стьюдента. Это значение составляет: t _α = 2,145 (при уровне значимости α = 0,05 и числе степеней свободы, с которым определялась дисперсия воспроизводимости m = 7(3 − 1) = 14). C учетом табличного значения t _α доверительный интервал коэффициента регрессии находится по формуле:

В связи с тем, что в данном случае значение коэффициента регрессии по абсолютной величине превышает доверительный интервал = 0,5125 > Δ k = 0,0217, этот коэффициент можно считать значимым, а наличие зависимости y = f(x) − статистически подтвержденным фактом.

Значимость свободного члена в уравнениях регрессии, как правило, не проверяют, считая его значимым при любых условиях. Таким образом, в данном случае имеем два значимых коэффициента уравнения регрессии (L = 2). Дисперсию адекватности принятой математической модели рассчитаем с учетом данных табл. 2 по формуле:

Фактическое значение критерия Фишера рассчитаем как отношение:

Табличное значение критерия Фишера при уровне значимости α = 0,05 и числах степеней свободы, с которыми определялись дисперсии адекватности (m ₁ = N – L = 5) и воспроизводимости (m ₂ = N(n –1) = 14), cоставляет Fтаб = 2,96. Так как F < Fтаб, полученное уравнение регрессии (10) адекватно с уровнем доверительной вероятности Р = 1 − α = 0,95.

Регрессионный анализ и ортогональное планирование первого