Научные основы физического моделирования

Геометрическое подобие является одной из форм подобия физических процессов. Оно рассматривается как первое необходимое условие моделирования реальных объектов. Геометрическое подобие модели и натуры должно соблюдаться при решении любых экспериментальных задач, к какому бы классу явлений они ни относились. Условием геометрического подобия является пропорциональность всех сходственных линейных размеров объектов.

Условие кинематического подобия означает, что в сходственных точках геометрически подобных систем все скорости движущейся среды υ, м/с, параллельны и пропорциональны.

Динамическое подобие заключается в том, что в сходственных точках геометрически подобных объектов силы f, Н, действующие на жидкость, параллельны и пропорциональны.

Тепловое подобие заключается в том, что в сходственных парах точек геометрически подобных объектов разности температур Δ t, °С, пропорциональны.

Теоремы теории подобия. Теория подобия физических явлений основана на трех основных теоремах [12]. Первая из них, называемая теоремой Ньютона, определяет необходимые условия подобия и формулируется следующим образом: у подобных явлений в любых парах сходственных

точек все одноименные критерии подобия численно одинаковы.

Вторая теорема подобия называется теоремой Федермана. Она формулируется следующим образом: решение любой системы дифференциальных уравнений всегда может быть представлено в виде некоторой функциональной зависимости между рядом безразмерных критериев. Эта зависимость будет единой для целой группы подобных явлений.

Третья теорема подобия – теорема Кирпичева-Гухмана определяет достаточные условия подобия и является научной основой физического моделирования явлений. Она формулируется следующим образом: подобными будут те явления, условия однозначности которых подобны, а

критерии, составленные из величин, входящих в условия однозначности (то есть определяющие критерии), равны. Согласно этой теореме, если обеспечить взаимное равенство всех определяющих критериев для каких-либо двух явлений, то эти явления обязательно окажутся подобными. Такой вывод следует из совместного применения первой и второй теорем.

Разработка физических моделей. С учетом всего вышеизложенного можно сделать несколько обобщающих выводов, помогающих уяснить основные принципы моделирования физических процессов и расчета констант подобия, необходимых для создания физических моделей.

1. Если два каких-либо процесса подобны, то любая из определяющих размерных физических величин а ′′, b ′′, с ′′…., измеренная в заданной точке модели, всегда пропорциональна соответствующей физической величине а ′, b ′, с ′…. в сходственной точке реального процесса, то есть

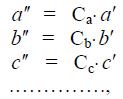
где Са; Cb; Cc….. – безразмерные константы подобия соответствующих физических величин.

Однако численные значения констант подобия для разноименных физических величин в пределах одной модели различны: Са ≠ Cb ≠ Cc …..

2. При исследовании любых физических процессов из определяющих размерных величин а, b, с ….. всегда может быть образован ряд безразмерных определяющих критериев π i. Каждый из критериев может быть представлен в виде произведения входящих в него размерных физических величин в некоторых определенных степенях α, β, γ…, то есть

3. Одноименные определяющие критерии подобных процессов должны быть одинаковыми, а их отношение – равным 1, следовательно

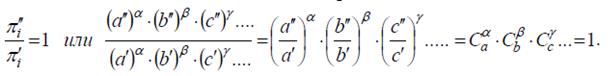
Последнее выражение является общей формулой взаимосвязи констант подобия физических величин при моделировании реальных процессов.

Методы теории подобия дают возможность получения безразмерных критериев подобия путем математических преобразований любых сколь угодно сложных систем дифференциальных уравнений, описывающих физические процессы в исследуемом объекте. Однако эта теория неприменима к изучению процессов, точное математическое описание которых не известно. Поэтому при исследовании таких процессов для получения безразмерных критериев и обоснования общего вида критериальных зависимостей используется метод анализа размерностей.

III. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЯХ И ОСНОВЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА