Соединение фаз приемников схеме четырехпроводная звезда

При соединении фаз приемника по схеме звезда их концы х, у, z соединяют в одну общую точку «n» (рис. 140.), которую соединяют с помощью нейтрального провода с нейтральной точкой генератора " N ".

Рисунок 140. Соединение фаз приемников схеме четырехпроводная звезда

В соответствии с рисунком 140:

А, В, С – начала фаз генератора;

N – общая нейтральная точка соединения фаз генератора;

а, в, с - начала фаз приемника;

х, у, z – концы фаз приемника;

n – общая нейтральная точка соединения фаз приемника;

R_a, R_B, R_C – активные сопротивления фаз приемника.

Провода, соединяющие начала фаз генератора (А, B, C) с началом фаз приемника (а, в, с), называются линейными проводами.

Соответственно, ток I_N, протекающий по нейтральному проводу, называется нейтральным, а токи I_A, I_B, I_C протекающие по линейным проводам - линейными. Для схемы звезда линейные токи одновременно являются фазными токами, протекающими по фазам приемника.

I_Л=I_Ф.

За положительное направление фазных токов условно принимают направление от генератора к приемнику, а за положительное направление нейтрального тока - от приемника к генератору.

Напряжения U_a, U_в, U_с между началом и концом фаз приемника называют фазными, а напряжения U_АВ, U_ВС, U_СА между началами фаз или между двумя линейными проводами - линейными напряжениями.

За условное положительное направление фазного напряжения принято направление от начала к концу фаз приемника (генератора). Условные положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу.

Линейные напряжения связаны с фазными напряжениями, следующими уравнениями: 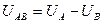, , (16.2)

Отметим, что уравнения (16.2) позволяют определить значения линейных напряжений, как для симметричной, так и для несимметричной систем напряжений. В соответствии с этими уравнениями на рис. 141 построена топографическая векторная диаграмма фазных и линейных напряжений.

Рисунок 141. Векторная диаграмма фазных и линейных напряжений для схемы звезда.

Из диаграммы видно, что для симметричной системы фазных напряжений линейные напряжения представляются тремя векторами, сдвинутыми относительно друг друга по фазе на 120°. Величина каждого из векторов линейного напряжения будет в раз больше величины фазного напряжения:

(3)

Предусмотренные ГОСТом номинальные напряжения и применяемые на практике для цепей низкого напряжения величины напряжений 127 В, 220 В, 380 В, 660 В как раз и отличается друг от друга в =1,73 раза.

Расчет токов в фазах осуществляется на основе следующих соотношений:

,

, (16.4)

.

Угол сдвига фаз между фазными токами и напряжениями определяется характером нагрузки и в общем случае может быть вычислен по формулам

,

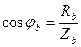, (16.5)

,

где: R_a, R_в, R_c — активные сопротивления фаз приемника.

Расчет тока в нейтральном проводе производится на основании первого закона Кирхгофа согласно векторному уравнению

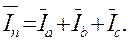(16.6)

Рассмотрим пример расчета трехфазной цепи, соединенной по схеме четырехпроводная звезда, если:

Z_a>Z_b>Z_c.

φ_a=0, φ_b<0, φ_c>0.

Согласно (16.4) между величинами фазных токов будет справедливо следующее соотношение:

I_a>I_b>I_c.

Так как φ_а= 0, нагрузка в фазе " а " будет носить чисто активный характер/ В фазе " в " φ_в< 0, тогда нагрузка имеет активно-емкостный характер. В фазе " с " φ _с> 0, тогда нагрузка имеет активно-индуктивный характер.

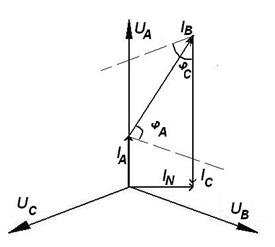
Рисунок 142. Векторные диаграммы токов и напряжений при разнородной несимметричной нагрузке

На рисунке 142 построены векторные диаграммы фазных напряжений и фазных токов для данного случая разнородной несимметричной нагрузки.

Построение векторной диаграммы токов производилось в следующем порядке:

_1. Из точки " n " строится вектор тока I_а, совпадающий с направлением вектора фазного напряжения U_a.

_2. Из конца вектора I_а под углом φ_в к вектору U_e строится вектор тока I_в. Угол φ_в откладывается против часовой стрелки, т. к. при активно-емкостной нагрузке ток опережает напряжение.

_3. Из конца вектора I_в под углом φ_с к вектору U_c строится вектор I_С. Угол φ_с откладывается по часовой стрелке, т. к. при активно-индуктивной нагрузке ток отстает от напряжения.

_4. Вектор I_п тока в нейтральном проводе строится из начала вектора I_а в конец вектора I_С.

1.3. Соединение фаз приемника по схеме «треугольник»

Кроме соединения в звезду широкое применение получили трехпроводные трехфазные цепи с соединением приемников в треугольник.

Если три фазы приемника с фазными сопротивлениями включить непосредственно между линейными проводами трехпроводной цепи, то получим соединение приемников в треугольник (рис. 143).

Рисунок 143.Соединение фаз приемника по схеме «треугольник»

Из схемы видно, что если пренебречь сопротивлениями линейных проводов, то независимо от характера нагрузки напряжение на каждой фазе приемника равно линейному напряжению:

.

Но фазные и линейные токи (в отличие от схемы соединения в звезду) не равны между собой. За положительное направление фазных токов I_аb, I_bс, I_са принято направление от начала к концу фазы. Если напряжения и сопротивления фаз нагрузки заданы, то фазные токи определяются по формулам:

(16.7)

Угол сдвига фаз между фазными токами и напряжениями определяется характером нагрузки и в общем случае может быть вычислен по формулам

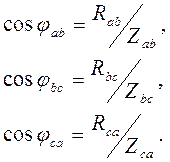, (16.8)

где: R_aв, R_вc, R_ca - активные сопротивления фаз приемника.

Линейные токи определяются по фазным токам из уравнений, составленных по первому закону Кирхгофа для узлов а, в, с:

(16.9)

Из уравнений (9) следует, что любой из линейных токов равен геометрической разности токов тех двух фаз нагрузки, которые соединяются с данным линейным проводом, а также следует, что независимо от характера нагрузки геометрическая сумма линейных токов в трехпроводной цепи равна нулю.

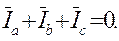
Рассмотрим пример расчета трехфазной цепи при соединении фаз приемника по схеме треугольник для случая, когда

Z_ab>Z_bc>Z_ca. (16.10)

φ_ab=0, φ_bc<0, φ_ca>0.

Согласно (16.7) между фазными токами будет справедливо следующее соотношение:

I_ab>I_bc>I_ca.

Так как φ_аb = 0, поэтому нагрузка в фазе " аb " будет носить чисто активный характер. В фазе " bс " φ_bc< 0 и нагрузка имеет активно-индуктивный характер. В фазе " са " φ_ca> 0 инагрузка имеет активно-емкостный характер.

На рис. 144. построена векторная диаграмма линейных напряжений и фазных и линейных токов для данного случая.

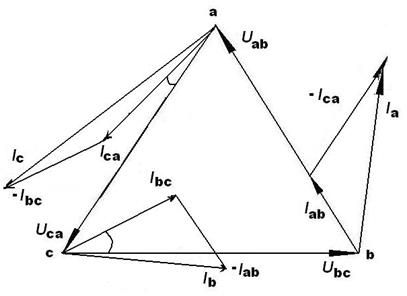
Рисунок 144. Векторные диаграммы токов и напряжений при разнородной несимметричной нагрузке: Z_ab>Z_bc>Z_ca, φ_ab=0, φ_bc<0, φ_ca>0