
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример расчета электрической цепи со смешанным соединением элементов
|
|
Рассмотрим порядок расчета электрической цепи соответствующей варианту 72.
Дано:
R1=0 Ом, R2=20 Ом,
XL1.1=10 Ом, XC2.1=0,
XC1=40 Ом, XL2=20 Ом,
XL1.2=0 Ом, XC2.2=0 Ом..
Данному варианту соответствует электрическая схема рис. 136.

Рисунок 136. Электрическая схема цепи, согласно варианту 3
Расчет производится в следующем порядке:
1. Определяем полное сопротивление первой ветви:
 Ом.
Ом.
2. Определяем полное сопротивление второй ветви:
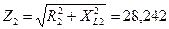 Ом.
Ом.
Примечание: расчет вести до четырех значащих цифр.
3. Определяем активную проводимость первой ветви:
 .
.
4. Определяем реактивную проводимость первой ветви:
 См.
См.
5. Определяем полную проводимость первой ветви:
 См.
См.
6. Определяем активную составляющую первого тока:
 .
.
7. Определяем реактивную составляющую первого тока:
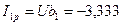 А.
А.
8. Определяем полный ток первой ветви:
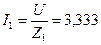 А.
А.
9. Определяем активную проводимость второй ветви:
 См.
См.
10. Определяем реактивную проводимость второй ветви:

 См.
См.
11. Определяем полную проводимость второй ветви:
 См.
См.
12. Определяем активную составляющую тока второй ветви:
 А.
А.
13. Определяем реактивную составляющую тока второй ветви:
 А.
А.
14. Определяем полный ток второй ветви:
 А.
А.
15. Определяем активную проводимость всей цепи:
 См.
См.
16. Определяем реактивную проводимость всей цепи:
 См.
См.
17. Определяем полную проводимость всей цепи:
 См.
См.
18. Определяем активную составляющую тока в неразветвленной части цепи:
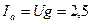 A.
A.
19. Определяем реактивную составляющую тока в неразветвленной части цепи:
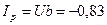 A.
A.
20. Определяем полный ток в неразветвленной части цепи:
 A.
A.
21. Определяем коэффициент мощности первой ветви:
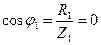 .
.
22. Определяем коэффициент мощности второй ветви:
 .
.
23. Определяем коэффициент мощности всей цепи:
 .
.
24. Определяем полную мощность первой ветви:

 В.
В.
25. Определяем активную мощность первой ветви:
 .
.
26. Определяем реактивную мощность первой ветви:
 ВАр.
ВАр.
27. Определяем полную мощность второй ветви:

 В.
В.
28. Определяем активную мощность второй ветви:
 Вт.
Вт.
29. Определяем реактивную мощность второй ветви:
 ВАр.
ВАр.
30. Определяем полную мощность всей цепи:

 В.
В.
31. Определяем активную мощность всей цепи:
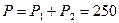 Вт.
Вт.
32. Определяем реактивную мощность всей цепи:
 ВАр.
ВАр.
33. Векторная диаграмма токов (рис 137)строится на основании первого закона Кирхгофа для цепей синусоидального тока:
 .
.
Векторная диаграмма токов строится в следующем порядке:
33.1 За базовую ось принимаем вектор напряжения U, который является общим для обеих параллельных ветвей. Строим этот вектор горизонтально в масштабе mU.
33.2 По активной и реактивной составляющей первого тока строится вектор тока I1. Но так как активная составляющая первого тока I1a=0, то полный ток I1 будет равенреактивной составляющей I1р, которая имеет емкостный характер и опережает вектор напряжения U на угол 90° (X=XL1.1 – XC1<0). Этот вектор строим перпендикулярно к вектору напряжения U против часовой стрелки (φ1=-90°) в масштабе m1.
33.3 Аналогично строим вектор тока второй ветви. Активная составляющая тока I2a совпадает по фазе с вектором напряжения U, реактивная составляющая тока второй ветви I2р носит индуктивный характер (X2=XL2>0) и отстает от вектора напряжения U на угол 90°. Этот вектор строим перпендикулярно к вектору напряжения по часовой стрелке. Вектор полного тока второй ветви будет равен диагонали параллелограмма построенного на векторах I2a и I2р.
34. Векторная диаграмма напряжений для первой ветви строится на основании второго закона Кирхгофа:
 .
.
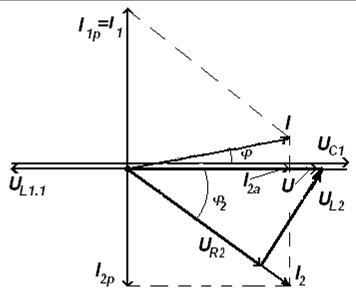
Рисунок 137. Векторная диаграмма токов и напряжений
Векторная диаграмма напряжений строится в следующем порядке:
34.1 Строится вектор падения напряжения на индуктивном сопротивлении XL1.1, модуль которого равен:
 B.
B.
На индуктивности напряжение опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I1 против часовой стрелки.
34.2 Из конца вектора UL1.1 строится вектор падения напряжения на емкостном сопротивлении XC1, модуль которого равен:
 B.
B.
На емкости напряжение отстает от тока на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I1 по часовой стрелке. Если вычисления и построения сделаны верно, то конец вектора UC1 будет совпадать с концом вектора U.
35. Векторная диаграмма напряжений для второй ветви строится на основании второго закона Кирхгофа:
 .
.
Векторная диаграмма напряжений для второй ветви строится в следующем порядке:
35.1 Строится вектор падения напряжения на активном сопротивлении R2, модуль которого равен
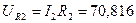 B.
B.
На активном сопротивлении напряжение и ток совпадают по фазе, поэтому этот вектор падения напряжения строим совпадающим по направлению с вектором тока I2.
35.2 Из конца вектора UR2 строится вектор падения напряжения на индуктивном сопротивлении XL2, модуль которого равен:
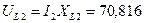 B.
B.
Напряжение на индуктивности опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I2 против часовой стрелки.
Если вычисления и построения сделаны верно, конец вектора напряжения UL2 будет совпадать с концом вектора U.
Рекомендуемый масштаб:
mu=1B/мм,
mI=0,05А/мм.
36. Для обеспечения резонанса токов в электрической схеме с двумя параллельными ветвями должны выполняться следующие условия:
· параллельные ветви должны иметь разный характер проводимостей (одна индуктивный, другая емкостный).
· реактивные проводимости параллельных ветвей должны быть равны по модулю, т.е.:
 .
.
В данном варианте первое условие выполняется, т.к. первая ветвь носит емкостный, а вторая – активно-индуктивный характер.
Для достижения резонанса токов, т.к. 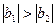 необходимо в первую ветвь включить дополнительно емкость, величину сопротивления которого можно вычислить следующим образом:
необходимо в первую ветвь включить дополнительно емкость, величину сопротивления которого можно вычислить следующим образом:
 См,
См,
 ,
,
 Ом.
Ом.
37. После включения дополнительной емкости в первую ветвь изменится ток в этой ветви и падения напряжения на индуктивности и емкости.
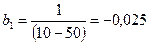 См,
См,
 А,
А,
 А,
А,
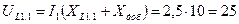 В,
В,
 В.
В.
Векторная диаграмма, построенная аналогично п.п. 33-35, представлена на рис. 138.
Рекомендуемый масштаб:
mu=1B/мм,
mI=0,05А/мм.

Рисунок 138. Векторная диаграмма токов и напряжений для случая резонанса токов
Таблица15.1
| № | Величина сопротивления (Ом) | ||||||||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||
| № | Величина сопротивления (Ом) | ||||||||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||
| Величина сопротивления (Ом) | |||||||||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||
XVI. КОНТРОЛЬНАЯ РАБОТА №2. Расчёт трёхфазной электрической цепи синусоидального тока
ПОСТАНОВКА ЗАДАЧИ
Задачей расчета трёхфазных электрических цепей являются установление связи между линейными и фазными токами, мощностями и напряжениями фаз и всей трёхфазной цепи, ЭДС, сопротивлениями токоприёмников, определив которые, можно рассчитать коэффициент мощности, сечения проводников для питания конкретной электроустановки, а также рассчитать параметры электрических устройств (емкость конденсаторов) для повышения коэффициента мощности электроприемников.
Для того чтобы провести анализ конкретной электрической установки, как правило, данную электроустановку представляют в виде эквивалентной электрической схемы замещения, состоящей из источников ЭДС, напряжений и активных и реактивных сопротивлений (индуктивностей и конденсаторов). Результаты расчетов эквивалентной электрической схемы переносят на реальную электрическую установку.
Ввиду значительного объема информации по расчетам трёхфазных электрических цепей, в настоящих методических указаниях поставлена задача помочь студентам ориентироваться в методах анализа электрических цепей, дать рекомендации по методикам и особенностям расчета электрических цепей со смешанным соединением активных и реактивных элементов, рассмотрен порядок их выполнения.
Date: 2016-11-17; view: 1281; Нарушение авторских прав