Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
I. Лабораторная работа № 1. Исследование электрической цепи синусоидального тока при последовательном соединении активного, индуктивного и емкостного сопротивлений
ЦЕЛЬ РАБОТЫ
Изучение основных законов неразветвленной цепи переменного тока.
Освоение методики расчета и построения векторных диаграмм при последовательном соединении элементов.
ПРЕДВАРИТЕЛЬНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Общие положения и определения.
Электромагнитный процесс в электрической цепи, при котором мгновенные значения напряжений и токов повторяются через равные промежутки времени, называется периодическим.
Наименьшее время, по истечении которого мгновенные значения периодической величины повторяются, называется период ом Т (с).
Величина, обратная периоду, т. е. число периодов в единицу времени, определяет частоту.
, 
.
Преобладающим видом процесса в электрических цепях является синусоидальный режим, характеризующийся тем, что все напряжения, токи и ЭДС являются синусоидальными функциями одинаковой частоты рис. 1.
где- u, i, e — мгновенные значения соответствующей периодической величины;
, 
, 
— максимальные (амплитудные) значения;
— скорость изменения (угла), называемая угловой частотой:
, 
.
Аргумент функции вида 
, определяющий стадию изменения синусоидальной величины, называется фазовым углом или фазой, а 
, 
, 
— начальная фаза (при t = 0), определяется смещением синусоиды, относительно начала координат, она измеряется абсциссой точки перехода отрицательной полуволны в положительную.
Рисунок 1. Временные диаграммы тока, напряжения и ЭДС
При совместном рассмотрении нескольких синусоидальных функций одной частоты разность их фаз, равной разности начальных фаз, называют угл ом сдвига фаз (
).
Например, угол сдвига фаз между напряжением и током
.
Следует отметить, что мгновенные значения токов, напряжений и ЭД С не показательны в оценке их величин.
Синусоидальную функцию времени можно изобразить вектором, равным амплитуде данной функции, равномерно вращающимся с угловой скоростью ω. При этом начальное положение вектора определяется (для t=0) его начальной фазой 
(см. рис. 2).
Рисунок 2. Вращающийся вектор тока 
и график изменения тока 
во времени
При изображении синусоидальной ЭДС, напряжений и токов из начала координат проводят векторы, равные амплитудным значениям этих величин, под углом 
к горизонтальной оси. Положительные углы откладываются против часовой стрелки.
Если вращать вектор против часовой стрелки, то в любой момент времени он составит с горизонтальной осью угол, равный 
. Проекция вращающегося вектора на ось ординат (ось мгновенных значений) равна мгновенному значению синусоидальной величины.
Совокупность векторов на плоскости, изображающих ЭДС, напряжения, токи одной частоты, называют векторной диаграммой.
При исследовании установившихся режимов векторы неподвижны, их длина равна действующим значениям электрических величин.
С помощью векторов можно производить геометрическое суммирование электрических величин.
Так, на рисунке 3. показан вектор I m расположенный в начальный момент (t=0) к исходной оси под углом j, равным начальной фазе и вращающийся в положительную сторону с угловой частотой w. Тогда проекция этого вектора на ось ординат будет равна мгновенному значению функции для этого момента времени, соответствующего положению этого вращающегося вектора. Угол yi обозначает начальную фазу тока.
Рисунок 3. Диаграмма вращающегося вектора тока
Векторные диаграммы широко используются при анализе электрических цепей переменного тока.
Переменный ток обычно характеризуется его действующим или среднеквадратичным значением 
:
.
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Действующее значение переменного тока i равно такому постоянному току, который за время одного периода Т выделит в сопротивлении столько тепла, что и переменный ток
Аналогично:
.
Номинальные токи и напряжения электрических устройств определяются, как правило, действующими значениями. Приборы электромагнитной, электродинамической и тепловой систем показывают действующие значения периодически изменяющихся величин.
2.2. Электрические цепи с активным сопротивлением, индуктивностью и ёмкостью
В цепях с изменяющимися во времени токами, кроме процессов преобразования электроэнергии в другие виды энергии, наблюдаются процессы, обусловленные изменением энергии магнитных и электрических полей. Чтобы учесть эти процессы при построении электрических схем, используют три параметра: активное сопротивление R, индуктивность L, емкость С, характеризующие такие элементы цепи, как резисторы, катушки и конденсаторы.
Сопротивление цепи переменного тока, в котором происходит необратимое преобразование электрической энергии в тепловую, называется активным сопротивлением R.
В цепи с активным сопротивлением рис. 4, а ток совпадает по фазе с приложенным напряжением, т.е. =0 (рис. 4, б, в)
Рисунок 4. Схема (а), временная (б), и векторная диаграммы цепи с резисторным элементом
Действующие значения тока и напряжения связаны законом Ом а:
.
Индуктивным элемент омназывается идеализированный элемент электрической цепи (
), приближающийся по свойствам к индуктивной катушке, в которой накапливается энергия магнитного поля. При этом термин «индуктивность» характеризует свойство цепи накапливать энергию магнитного поля. Она является количественной оценкой отношения потокосцепления 
рассматриваемого контура к току, его создающему:
.
При переменном токе сопровождающее его магнитное поле изменяется во времени. На основании закона электромагнитной индукции Фарадея-Максвелла появляется ЭДС самоиндукции
.
По закону Ленца, выражающему принцип электромагнитной инерции, эта ЭДС противодействует изменению потокосцепления, что и учитывается знаком минус.
Если L не зависит от i, т.е. рассматриваемая цепь линейна, то
.
Величина:
называется падением напряжения в индуктивности. Для цепи с индуктивностью (рис. 5, а), где
т. е. индуктивное падение напряжения опережает ток на 90° (рис. 5, б, в).
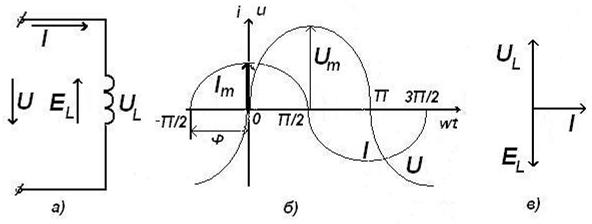
Рисунок 5. Схема (а), временная (б), и векторная диаграммы цепи с индуктивной катушкой
Действующее значение напряжения
.
Величину 
принято называть реактивным индуктивнымсопротивлением и обозначается через XL
, [ Ом ].
При рассмотрении реальных катушек необходимо учитывать, что в отличие от идеальных, их активное сопротивление RL не равно 0.
Емкость учитывает влияние изменяющегося электрического поля элементов цепи и может быть определена как отношение заряда к напряжению на емкостном элементе:
.
При включении емкости при напряжение 
(рис. 6, а) в цепи появляется ток:
Следовательно, ток опережает напряжение на емкости на 90°(рис. 6, б, в)
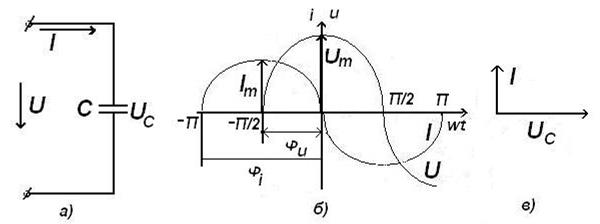
Рисунок 6. Схема (а), временная (б), и векторная диаграммы цепи с идеальным конденсатором
Действующее значение тока:
.
Величина 
, имеющая размерность сопротивления (Ом), называется реактивным емкостным сопротивлением и обозначается XC: 
.
2.3. Последовательное соединение элементов с параметрами R, L, С
Схема неразветвленной цепи синусоидального тока представлена на рис. 7. Энергетическое состояние цепи описывается для мгновенных значений уравнением:
, 
,
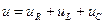Рисунок 7. Схема последовательного соединения элементов цепи
Если то напряжение на входных зажимах будет также изменяться по синусоидальному закону в силу линейности рассматриваемой цепи. После несложных преобразований дифференциальное уравнение цепи можно привести к виду:
Это уравнение позволяет построить временную диаграмму, которая полностью отражает амплитудные и фазовые соотношения в последовательной цепи. Для практических расчетов применяют векторные диаграммы, которые делают расчет цепи более наглядным и простым.
Под векторной диаграммой цепи понимают совокупность векторов ЭДС, напряжений и токов электрической цепи, построенных с соблюдением их взаимной ориентации по фазе. Так как чаще при анализе и расчете электрической цепи пользуются действующими значениями токов и напряжений, векторную диаграмму, как графическую интерпретацию расчета цепи, строят также для действующих значений напряжений и токов. При построении векторной диаграммы в качестве исходного вектора удобнее выбрать вектор величин, одинаковой для нескольких элементов цепи. В последовательной цепи (рис. 7) по всем участкам проходит один и тот же ток, поэтому за исходный вектор выбирается вектор тока и относительно его строятся под углом сдвига векторы напряжений на всех участках.
На топографической векторной диаграмме каждая точка соответствует определенной точке электрической цепи. Чтобы осуществить это соответствие точек диаграммы и цепи, построение векторов топографической диаграммы ведут в той же последовательности, в какой обходят электрическую цепь. На рис. 8 показана топографическая диаграмма для цепи рис. 7.
Обход цепи начат от точки «d». При переходе к точке «с» потенциал увеличивается на величину падения напряжения на емкости 
Вектор этого падения напряжения 
отстает от вектора тока I на угол 90°. Потенциал точки «в» выше потенциала точки «с» на величину падения напряжения на втором участке, вектор которого 
опережает по фазе вектор тока на угол 90°. Потенциал точки «а» выше потенциала точки «в» на величину падения напряжения 
вектор, которого совпадает с вектором тока. Вектор результирующего напряжения расположен между точками «а» и «d».
Рисунок 8. Векторная диаграмма токов и напряжений при последовательном соединении элементов цепи
В зависимости от величин L и С возможны следующие варианты: XL>XC; XL<XC; XL=XC.
Для варианта XL>XC , угол φ>0, UL>UC. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный характер. Векторная диаграмма напряжений имеет вид как на рис. 9.
Рисунок 9. Векторная диаграмма напряжений для варианта XL>XC , угол φ>0, U L> U C
Для варианта XL<XC угол φ<0, UL<UC. Ток опережает напряжение на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид как на рис.10.
Рисунок 10. Векторная диаграмма напряжений для варианта XL<XC угол φ<0, U L< U C
Для варианта XL=XC , угол φ=0, UL=UC. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление Z=R наименьшее из всех возможных значений XL и XC. Векторная диаграмма напряжений имеет вид (рис.11).
Рисунок 11. Векторная диаграмма напряжений для варианта XL=XC , угол φ=0, UL=UC
Этот режим называется резонанс напряжений (UL=UC). Напряжения на элементах UL и UC могут значительно превышать входное напряжение.
На векторной диаграмме рис. 9 или рис. 10 можно выделить треугольник, который принято называть треугольник ом напряжения. В этом треугольнике:
где 
‑ активная составляющая напряжения;
— реактивная составляющая напряжения.
Очевидно:
Поделив модули вектора треугольника напряжений на ток, получим подобный ему треугольник сопротивлений рис. 12.,
Рисунок 12. Треугольник сопротивлений
где:
– активное сопротивление цепи;
- реактивное сопротивление цепи;
- полное сопротивление цепи.
От треугольника напряжений легко перейти также к треугольнику мощностей рис. 13.
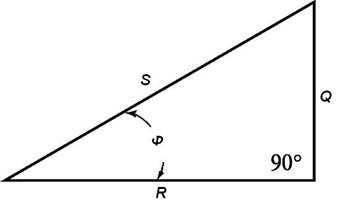
Рисунок 13. Треугольник мощностей.
В этом треугольнике:
‑ активная мощность цепи
‑ реактивная мощность цепи
‑ полная мощность цепи
называется коэффициент ом мощности цепи. Используя векторную диаграмму (см. рис. 8) можно написать аналитические выражения для мгновенных значений тока и напряжений. Так для рис. 7, если:
то
.
.
Последовательная цепь может содержать большое число приемников с различными значениями R, L, С.
При этом активные сопротивления, напряжения и мощности отдельных приемников складываются арифметически:
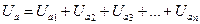
Реактивные сопротивления, напряжения и мощности отдельных приемников складываются алгебраически:
при этом величины, относящиеся к индуктивности, входит в сумму со знаком «плюс», а величины, относящиеся к емкости со знаком «минус». Полные сопротивления, напряжения и мощности отдельных приемников складываются геометрически.
Date: 2016-11-17; view: 1219; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |