Теория потребительского выбора.

1.1. Количественный (кардиналистский) подход к анализу полезности и спроса. Количественный подход к анализу полезности основан на представлении о возможности измерения различных благ в гипотетических единицах полезности - ютилах (от англ. utility - полезность).

В частности, предполагается: потребитель может сказать, что ежедневное потребление им 1 яблока приносит ему удовлетворение, скажем, в 20 ютилов, ежедневное потребление 2 яблок и 1 сигареты - 50 ютилов и т.д. Количественный подход не предполагает возможности объективного измерения полезности того или иного товара в ютилах. Один и тот же продукт может представлять большую ценность для одного потребителя и никакой ценности - для другого. В приведенном выше примере речь идет, видимо, о заядлом курильщике, поскольку добавление к 2 яблокам 1 сигареты существенно увеличило полезность товарного набора. Количественный подход обычно не предусматривает также возможности соизмерения объемов удовлетворения, получаемых различными потребителями.

Экономисты неоднократно пытались избавиться от термина "полезность", имеющего некоторый оценочный характер, найти ему подходящую замену. Так, известный русский экономист Н. X. Бунге предлагал использовать термин "годность". Французский экономист Ш. Жид предлагал использовать термин "желаемость" (desirabilite - фр.), считая, что он "не предполагает у желания нравственных или безнравственных черт, разумных или безрассудных".

В поддержку термина "желаемость" высказывался и известный американский экономист и статистик И. Фишер. "Полезность, - считал он, - является наследием Бентама и его теории удовольствия и страдания". Тем не менее термин "полезность" пережил своих критиков и используется поныне. Итак, в количественной теории полезности предполагается, что потребитель может дать количественную оценку в ютилах полезности любого потребляемого им товарного набора. Формально это можно записать в виде функции общей полезности:

TU = F(Q_A, Q_B,..., Q_Z), (1.1)

где TU - общая полезность данного товарного набора; Q_A, Q_B, …, Q_Z - объемы потребления товаров А, В,..., Z в единицу времени. Большое значение имеют предположения о характере функции общей полезности. Рассмотрим, как изменяется общая полезность товарного набора в зависимости от объема потребления товара А (например, яблок). В верхней части рис. 1.1,a изображена эта зависимость. Длина отрезка ОК равна полезности товарного набора при фиксированных нами объемах товаров В, С,..., Z и при нулевом объеме потребления товара А. В количественной теории предполагается, что функция TU в верхней части рис. 3.1,а возрастающая (чем больше яблок, тем большую полезность имеет товарный набор) и выпуклая вверх (каждое последующее яблоко увеличивает общую полезность товарного набора на меньшую величину, чем предыдущее).

В принципе эта функция может иметь точку максимума (S), после которой она становится убывающей (представьте, что Вас ежемесячно заставляют потреблять по 100 кг яблок).

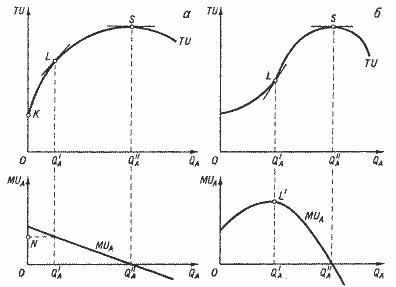
рис. 1.1. Общая и предельная полезность.

В нижней части рис. 1.1,а изображена зависимость предельной полезности яблок от объема их потребления.

1.2. Закон убывания предельной полезности. Предельная полезность - это прирост общей полезности товарного набора при увеличении объема потребления данного товара на одну единицу. Математически предельная полезность товара есть частная производная общей полезности товарного набора (1.1) по объему потребления г-того товара:

(1.2)

Геометрически значение предельной полезности (длина отрезка ON) равно тангенсу угла наклона касательной к кривой TU в точке L. Поскольку линия TU выпукла вверх, с увеличением объема потребления г-того товара угол наклона этой касательной уменьшается и, следовательно, понижается и предельная полезность товара. Если при некотором объеме его потребления (на нашем рисунке Q'_A) функция общей полезности достигает максимума, то одновременно предельная полезность товара становится нулевой.

Принцип убывающей предельной полезности часто называют первым законом Госсена, по имени немецкого экономиста Г. Госсена (1810-1859). Этот закон содержит два положения. Первое констатирует убывание полезности последующих единиц блага в одном непрерывном акте потребления, так что в пределе достигается полное насыщение этим благом. Второе констатирует убывание полезности первых единиц блага при повторных актах потребления. Принцип убывающей предельной полезности заключается в том, что с ростом потребления какого-то одного блага общая полезность, получаемая потребителем, возрастает, но возрастает все более медленно. Математически это означает, что первая производная функции общей полезности по количеству данного блага положительна, а вторая - отрицательна:

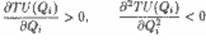(1.3)

Однако принцип убывающей предельной полезности отнюдь не универсален. Во многих случаях предельная полезность последующих единиц блага сначала увеличивается, достигает максимума и лишь затем начинает снижаться. Такая зависимость характерна для небольших порций делимых благ. Вторая затяжка выкуриваемой утром сигареты, возможно, имеет для любителя большую полезность, чем первая, а третья большую, чем вторая. Такая ситуация показана на рис. 1.1,б. В интервале от нуля до Q'_A общая полезность возрастает быстрее, чем увеличивается объем потребления блага, растет и предельная полезность. В интервале от Q'_A до Q'_A общая полезность растет медленнее, чем объем потребления, а предельная снижается от максимального уровня (в точке L') до нуля.

Математически это означает, что на участке от нуля до Q'_A и первая, и вторая частные производные функции общей полезности по объему потребления данного блага положительны:

(1.4)

Таким образом, принцип убывающей предельной полезности, или первый закон Госсена, справедлив лишь в том случае, если вторая частная производная функции общей полезности отрицательна. Однако поскольку потребитель покупает на рынке не отдельные акты потребления (в нашем примере), а определенные блага (в нашем примере - сигареты), мы можем считать, что для обращающихся на рынке товаров первый закон Госсена (1.3) выполняется.

Предположим теперь, что потребитель располагает некоторым доходом; цены на товары A, B,..., Z не зависят от его поведения и равны соответственно P_A, P_B, …,P_Z товарного дефицита нет; все товары являются бесконечно делимыми (как, например, колбаса, молоко и т.д.).

При этих предположениях потребитель достигнет максимума удовлетворения, если он распределит свои средства на покупку различных товаров таким образом, что:

1) для всех реально покупаемых им товаров А, В, С,... имеет место:

(1.5)

где MU_A, MU_B, MU_C - предельные полезности товаров А, В, С;  - некоторая величина, характеризующая предельную полезность денег;

2) для всех непокупаемых им товаров Y, Z,... имеет место:

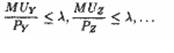(1.6)

Докажем первую часть утверждения.

Предположим обратное: товары А и В реально покупаются потребителем, но MU_A/P_A > MU_B/P_B. Для определенности предположим, что МU_A = 40 ютилов в расчете на килограмм, P_A = 2 руб. за килограмм, МU_B = 20 ютилов в расчете на килограмм, P_B = 4 руб. за килограмм. В результате:

(МU_A/P_A = 40 ютилов/2 рубля) > (20 ютилов/4 рубля = МU_B/P_B

Очевидно, что покупатель при этом не достигает максимума удовлетворения. Он может сократить потребление товара В на 1 кг, при этом он потеряет 20 ютилов. Но за счет сэкономленных 4 руб. он может купить дополнительно 2 кг товара А и получить дополнительно примерно 80 ютилов. Чистый выигрыш составит примерно 80 - 20 = 60 ютилов. С уменьшением потребления товара В его предельная полезность уменьшается.

Поэтому разница между МU_A/P_A и МU_B/P_B будет сокращаться. Перераспределение расходов будет происходить до тех пор, пока отношение предельной полезности к цене для каждого реально покупаемого товара не станет одинаковым. Равенство (1.5) можно интерпретировать следующим образом. Отношение МU_A/P_A представляет собой прирост общей полезности в результате увеличения расходов потребителя на товар A на 1 руб.

Очевидно, что в состоянии оптимума потребителя все подобные отношения для реально покупаемых товаров должны быть равны друг другу. И любое из них может рассматриваться как предельная полезность денег (точнее, 1 руб.).

Вторую часть утверждения можно доказать совершенно аналогичным образом, от противного. Смысл формулы (1.6) заключается в том, что если уже 1-й рубль, израсходованный на покупку товара Z, приносит потребителю недостаточно высокую полезность, то он вообще отказывается от потребления этого товара.

Таким образом, равенство (1.5) показывает, что в оптимуме (максимум полезности при данных вкусах потребителя, ценах и доходах) полезность, извлекаемая из последней денежной единицы, потраченной на покупку какого-либо товара, одинакова, независимо от того, на какой именно товар она израсходована. Это положение получило название второго закона Госсена.

1.3. Аксиомы порядкового (ординалистского) подхода к анализу полезности и спроса. Кривые безразличия. Порядковый подход к анализу полезности и спроса является более современным и основывается на гораздо менее жестких предположениях, чем количественный подход. От потребителя не требуется умения измерять полезность того или иного блага в каких-то искусственных единицах измерения. Достаточно лишь, чтобы потребитель был способен упорядочить все возможные товарные наборы по их "предпочтительности".

Порядковый подход базируется на следующих аксиомах.

1. Аксиома полной (совершенной) упорядоченности. Потребитель способен упорядочить все возможные наборы товаров с помощью отношений предпочтения (у) и безразличия (~). Это означает, что для любой пары товарных наборов А и В потребитель может указать, что либо А > В (А предпочтительнее, чем В), либо В > А (В предпочтительнее, чем А), либо А ~ В (А и В равноценны).

Данная аксиома не является слишком жесткой. Она лишь исключает возможность ответа "не знаю" на вопрос: "Какой из этих двух товарных наборов Вы предпочитаете?". Потребитель может выбрать любой из них либо сказать, что оба представляют для него одинаковую ценность.

2. Аксиома транзитивности. Если А > В > С, или А ~ В> С, или А > В ~ С, то А > С. Эта аксиома гарантирует согласованность предпочтений. Она, например, исключает возможность следующей ситуации: А > В, В > С и одновременно С > А.

Аксиома транзитивности содержит и еще одно утверждение, а именно: если А ~ В и В ~ С, то А ~ С. Пусть, например, индивидууму безразлично, положить в стакан чая 6 или 7 г сахарного песку, 7 или 8 г и т.д. Но тогда в силу только что высказанного утверждения ему должно быть безразлично, положить ли в него 6 или, скажем, 100 г сахара, что маловероятно.

3. Аксиома ненасыщения. Если набор А содержит не меньшее количество каждого товара, а одного из них больше, чем набор В, то А > В. Таким образом, предполагается, что увеличение потребления любого товара - при фиксированных объемах потребления других товаров - улучшает положение потребителя.

Если перевести эту аксиому на язык количественной теории полезности, то она исключает возможность нисходящей ветви линии TU на рис. 1.1 и отрицательных значений предельной полезности.

4. Аксиома независимости потребителя. Удовлетворение потребителя зависит только от количества потребляемых им благ и не зависит от количества благ, потребляемых другими.

Это прежде всего означает, что потребителю не знакомы чувства зависти и сострадания. В принципе и от этой аксиомы можно отказаться, что иногда и делается, в частности при анализе процессов потребления, сопровождающихся внешними эффектами и внешними затратами.

При порядковом подходе используются кривые и карта безразличия. Кривая безразличия - это множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. Если заполнить двухмерную плоскость кривыми безразличия так плотно, как это возможно, получим карту безразличия. На рис. 1.2 товарный набор А включает Х_А единиц товара X и Y_А единиц товара Y, товарный набор В включает Х_B единиц товара X и Y_B единиц товара Y. Если с точки зрения данного потребителя наборы А и В равноценны, то точки А и В лежат на одной и той же кривой безразличия.

рис. 1.2.Кривые безразличия.

Кривые безразличия обладают следующими свойствами.

А. Кривая безразличия, лежащая выше и правее другой кривой, представляет собой более предпочтительные для данного потребителя наборы товаров. Рассмотрим на рис. 1.2 кривые безразличия I и II. Набор С содержит такое же количество товара Y, что и набор А. Но набор С включает в себя большее количество товара X. Из аксиомы о ненасыщении следует, что С > А. Все наборы, лежащие на кривой безразличия I, с точки зрения нашего потребителя равноценны. То же относится и ко всем наборам, лежащим на кривой II. Из аксиомы о транзитивности следует, что любой набор, лежащий на кривой II, для нашего потребителя предпочтительнее любого набора, лежащего на кривой I.

Б. Кривые безразличия имеют отрицательный наклон. Пусть дана некоторая точка А (рис. 1.3), характеризующая определенную комбинацию товаров. Проведем через нее две взаимно перпендикулярные прямые. Очевидно, что все точки, лежащие в III квадранте, соответствуют большим, а все точки, лежащие в I квадранте, - меньшим количествам товаров X и Y, чем точка А. В соответствии с аксиомой ненасыщения точки, лежащие в III квадранте, более предпочтительны, а лежащие в I квадранте - менее предпочтительны, чем А. Следовательно, точки, безразличные А, например С, или В, или D, или G, должны находиться либо во II, либо в IV квадранте. И значит, кривая безразличия должна иметь отрицательный наклон.

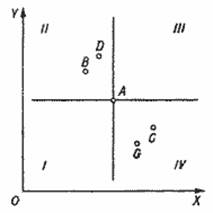
рис. 1.3.Кривые безразличия имеют отрицательный закон.

В. Кривые безразличия никогда не пересекаются. Предположим противное. Пусть кривые безразличия I и II на рис. 1.4 пересеклись в точке В. Из аксиомы о ненасыщении следует, что А > С. Наборы В и С лежат на одной кривой безразличия I. Поэтому В ~ С. Наборы А и В лежат на одной кривой безразличия II. Поэтому А ~ В. Из аксиомы о транзитивности следует, что А ~ С. Однако не могут одновременно быть А > С и А ~ С. Следовательно, кривые безразличия не могут пересекаться.

рис. 1.4. Невозможность пересечения кривых безразличия.

Заметим, что в отличие от непересекающихся прямых, которые должны быть параллельными, кривые могут не пересекаться и не будучи параллельными.

Г. Кривая безразличия может быть проведена через любую точку пространства товаров.

Д. Кривые безразличия выпуклы к началу координат. Это свойство в отличие от ранее перечисленных не может быть выведено непосредственно из аксиом рационального поведения. Оно просто отражает принцип диверсификации потребления.

Основным рабочим понятием порядковой теории полезности является предельная норма замещения. Предельной нормой замещения благом X блага Y(MRS_XY) называют количество блага Y, которое должно быть сокращено "в обмен" на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным:

(1.7)

Поскольку отношение Y/X по определению отрицательно, минус, вводимый перед правой частью, делает значение нормы замещения положительным.

рис. 1.5. Предельная норма замещения.

Пусть потребитель безразличен между наборами А и В (рис. 1.5, а). Значит, норма, по которой он согласен замещать благо Y благом X, оставаясь при этом на одной и той же кривой безразличия, составит:

(OY₁ - OY₂)/(OY₁ - OY₂) = - Y/X = -AK/KB

По мере приближения точки А к точке В отношение АК/КВ будет приближаться к наклону касательной в точке В. В пределе в окрестностях В наклон кривой (или касательной) в этой точке и есть предельная норма замещения:

(1.8)

Предельная норма замещения может принимать различные значения, она может быть равна нулю, может быть неизменной или меняться при движении вдоль кривой безразличия. В случае выпуклости к началу координат, как на рис. 1.5, MRS убывает по мере замещения одного блага другим, т.е. потребитель соглашается отдавать все меньшее количество замещаемого блага за одно и то же количество замещающего. Так, на рис. 1.5,б потребитель, находясь в точке А, готов уступить Y₀Y₁ блага Y взамен приращения блага X на X₀X₁. Однако, располагая набором С, он за равновеликое приращение блага X (X₂X₃ = X₀X₁) согласится уступить лишь Y₂Y₃ блага Y, что меньше Y₀Y₁.

1.4. Эффект замены и эффект дохода по Хиксу. Разложение общего эффекта изменения цены на эффект дохода и эффект замены по Хиксу показано на рис. 1.6. Бюджетная линия KL соответствует денежному доходу I и ценам Р_X и Р_Y. Ее касание с кривой безразличия U₁U₁ определяет оптимум потребителя E₁, которому соответствует объем потребления товара X в количестве Х₁. В случае снижения цены X до Р_Xt и неизменном денежном доходе I бюджетная прямая займет положение KL₁. Она касается более высокой кривой безразличия U₂U₂ в точке E₂, которой соответствует потребление товара X в объеме Х₂.

Таким образом, общий результат снижения цены товара X выражается в увеличении его потребления с Х₁ до Х₂.

рис. 1.6.Эффект замены и эффект дохода по Хиксу. Цена снижается.

При переходе от первоначального к дополнительному (расчетному) оптимуму (от E₁ к E₃) реальный доход потребителя не меняется, он остается на прежней кривой безразличия U₁U₁. Значит, сдвиг от E₁ к E₃ и характеризует эффект замены товара Y относительно подешевевшим товаром X. Он равен разности Х₃ - Х₁. Следовательно, эффект дохода составит Х₂ - Х₃- Заметим также, что в результате действия эффекта дохода потребление обоих товаров в точке E₂ выше, чем в точке E₃.

Такое же разложение общего эффекта может быть выполнено и для случая, когда цена товара X повышается (рис. 1.7). Здесь результатом повышения цены является перемещение оптимального положения потребителя на более низкую кривую безразличия U₁U₁. Общий эффект повышения цены товара X сводится к снижению его потребления с Х₁ до Х₂. При этом эффект замены составит Х₁ - Х₃, эффект дохода -Х₃ - Х₂. Заметим, что в обоих случаях эффект замены характеризуется движением вдоль одной и той же кривой безразличия, а эффект дохода - переходом с одной кривой на другую.

рис. 1.7.Эффект замены и дохода по Хиксу. Цена Х повышается.

Эффект замены всегда отрицательный. Снижение цены одного товара побуждает потребителя увеличивать его потребление, сокращая потребление другого товара (или группы товаров). Повышение цены побуждает его к замещению этого товара другими, относительно подешевевшими. Эффект дохода может быть отрицателен, как показано на рис. 1.6 и 1.7 для нормальных товаров, положителен (в случае некачественного товара, когда кривая доход-потребление имеет отрицательный наклон) или нейтрален (если кривая доход-потребление вертикальна).

1.5. Эффект замены и эффект дохода по Слуцкому. Подход Слуцкого к разложению общего результата изменения цены на эффект дохода и эффект замены отличается от подхода Хикса трактовкой реального дохода.

Элиминирование эффекта дохода достигается определением такого его уровня, который обеспечил бы потребителю возможность приобрести после изменения цен тот же самый набор товаров, что и до изменения, а не сохранить прежний уровень удовлетворения, как это предполагается в модели Хикса. Поэтому на рис. 1.8 вспомогательная бюджетная прямая K'L', параллельная KL₁, проводится не как касательная к прежней кривой безразличия U₂U₂, а строго через точку E₁, соответствующую оптимальному набору товаров X и Y при прежнем соотношении цен. Очевидно, она окажется касательной к более высокой, чем U₂U₂ кривой безразличия U₃U₃, что означает и возможность достигнуть (в случае полной компенсации потребителю падения его покупательной способности) более высокого уровня удовлетворения, чем при использовании модели Хикса. Таким образом, общий результат повышения цены товара X (Х₁ - Х₂) разлагается на эффект замены (Х₁ - Х₃) и эффект дохода (Х₃ - Х₂). Заметим, что движение от E₁ к E₂ происходит не вдоль кривой безразличия, как на рис. 3.16 и 3.17, а вдоль вспомогательной бюджетной прямой K'L'.

рис.1.8. Эффект замены и эффект дохода по Слуцкому. Цена Х повышается.

Сравнив два подхода, мы видим, что метод Хикса предполагает знание потребительских предпочтений, кривых безразличия, тогда как метод Слуцкого не требует этого, он базируется на наблюдаемых и регистрируемых фактах поведения потребителя на рынке.

Date: 2016-11-17; view: 453; Нарушение авторских прав