
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Проверка баланса мощностей
|
|
1) Составим баланс мощностей постоянной составляющей (нулевой гармоники):

где РП(0) – мощность приёмников;
РВ(0) – мощность источников.
Допустимая относительная погрешность расчётов:

Как видим, баланс мощностей сходится, значит, расчёт нулевой гармоники произведён верно.
2) Составим баланс мощностей для первой гармоники.
Полная вырабатываемая комплексная мощность всех источников ( ):
):

где  - сопряжённые значения токов источников.
- сопряжённые значения токов источников.

Суммарная активная мощность источников (РИСТ(1)):

Суммарная активная мощность приёмников ( ):
):


Допускается расхождение баланса активных мощностей:

Суммарная реактивная мощность источников (QИСТ(1)):

Суммарная реактивная мощность приёмников (QПР(1)):

где I1, I3 и 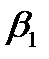 и
и  - действующие значения и фазы (углы) индуктивно связанных токов.
- действующие значения и фазы (углы) индуктивно связанных токов.
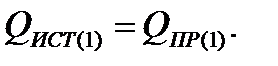
Допускается расхождение баланса активных мощностей:
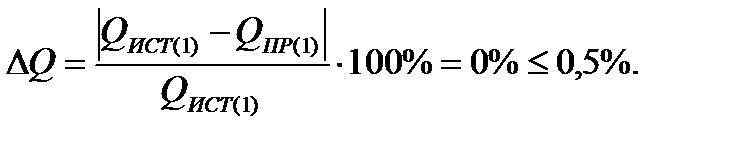
Так как баланс активных и реактивных мощностей сходится, то расчёт первой гармоники произведён верно.
3) Составим баланс мощностей для третьей гармоники.
Полная вырабатываемая комплексная мощность всех источников ( ):
):

где  - сопряжённые значения токов источников.
- сопряжённые значения токов источников.

Суммарная активная мощность источников (РИСТ(3)):

Суммарная активная мощность приёмников ( ):
):


Допускается расхождение баланса активных мощностей:

Суммарная реактивная мощность источников (QИСТ(3)):
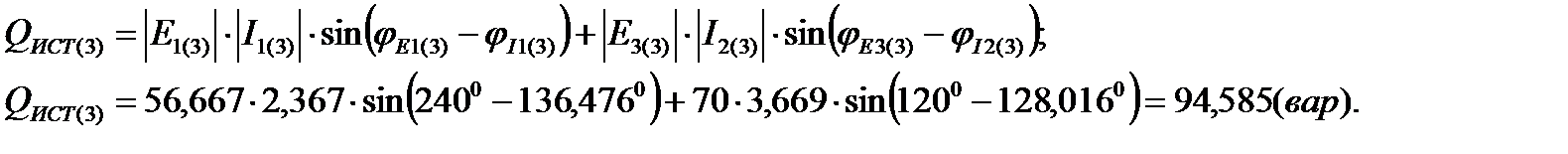
Суммарная реактивная мощность приёмников (QПР(3)):
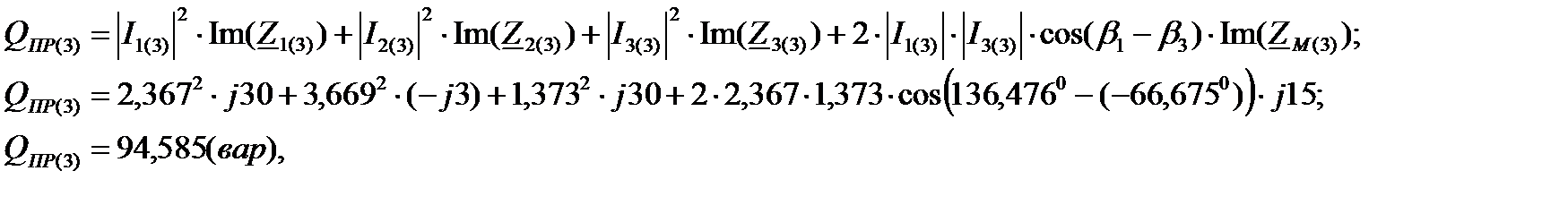
где I1(3), I3(3) и 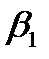 и
и  - действующие значения и фазы (углы) индуктивно связанных токов.
- действующие значения и фазы (углы) индуктивно связанных токов.

Допускается расхождение баланса активных мощностей:

Так как баланс активных и реактивных мощностей сходится, то расчёт третьей гармоники произведён верно.
4) Рассчитаем показатели энергетического процесса в цепи (баланс мощностей):
Активная мощность цепи равна сумме активных мощностей отдельных гармоник:

Реактивная мощность цепи равна сумме реактивных мощностей отдельных гармоник:

Полная мощность цепи:

В цепях с несинусоидальными источниками ЭДС должно выполняться неравенство:
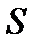 >
> 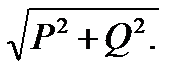
Проверим, выполняется ли данное неравенство:

6374>4918.
Неравенство выполняется.
4. Расчёт симметричной трёхфазной электрической цепи переменного тока
Для заданной схемы с симметричной системой фазных ЭДС, когда  и
и 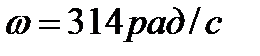 выполнить следующее.
выполнить следующее.
1. В симметричном режиме:
а) преобразовать схему до эквивалентной звезды и определить комплексы действующих значений напряжений и токов, а также рассчитать показание ваттметра;
б) в исходной схеме расчётом на одну фазу определить комплексы действующих значений всех напряжений и токов;
в) рассчитать балансы активной и реактивной мощностей;
г) построить совмещённые векторные диаграммы для всех напряжений и токов.
Исходные данные:
Таблица 1
| № | Е | 
|
| - | В | град |
| -30 |
Таблица 2
| № | R | L | C |
| - | Ом | мГн | мкФ |
| 318,47 | 31,8 |
Рис. 15 – Исходная схема
4.1. Расчёт фазных и линейных токов схемы
Расчёт симметричного режима трёхфазной цепи (рис.16).
Генератор симметричен, фазные ЭДС генератора:

Сопротивления реактивных элементов:

Обозначим сопротивления ветвей схемы:

Преобразуем треугольник сопротивлений  в эквивалентную звезду с сопротивлениями
в эквивалентную звезду с сопротивлениями  (рис.16):
(рис.16):
Рис.16 – Преобразование сопротивлений
Поскольку в симметричной цепи потенциалы нулевых точек (N, n1, n2) одинаковы, соединение этих точек нулевым проводом не нарушит режима цепи. Выделяем вместе с нулевым проводом одну фазу, например, А и сводим расчёт трёхфазной цепи к расчёту однофазной (рис.17). Токи и напряжения других фаз определяем с помощью фазового оператора.
Рис.17 – Однофазная цепь
Суммарное комплексное сопротивление фазы А:

Комплексные значения токов в ветвях фазы А по закону Ома:
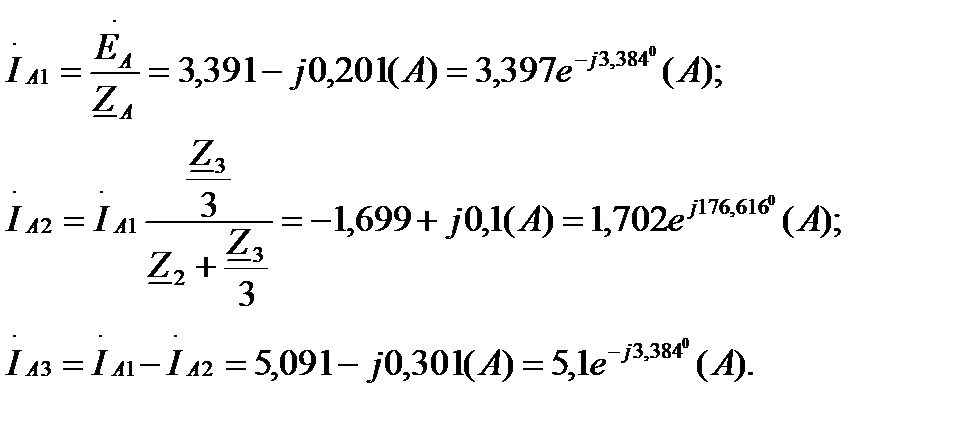
Комплексные значения токов в ветвях фазы В:
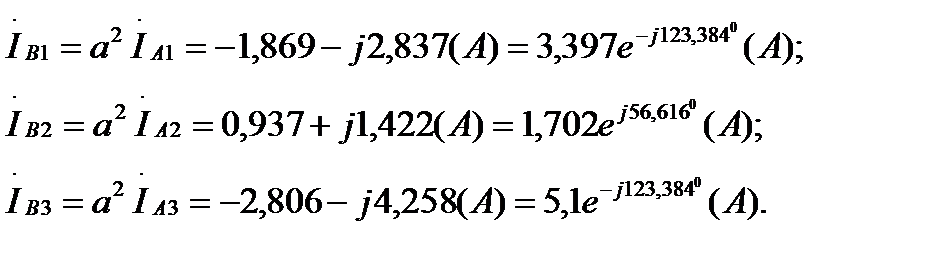
Комплексные значения токов в ветвях фазы С:

Определяем токи треугольника исходной схемы:

Таким образом, симметричный режим характеризуется симметричной системой фазных ЭДС и напряжений, а также одинаковой нагрузкой фаз. Трёхфазная цепь с одинаковой нагрузкой фаз называется симметричной.
Симметричный режим является нормальным режимом трёхфазных цепей и рассчитывается известными методами в комплексной форме.
Date: 2016-11-17; view: 1196; Нарушение авторских прав