
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Построение векторной диаграммы токов и напряжений
|
|
Для построения топографической диаграммы, совмещённой с векторной диаграммой токов, определим потенциалы узлов, при этом обозначим дополнительную точку на схеме k, потенциал точки «b» примем равным нулю:

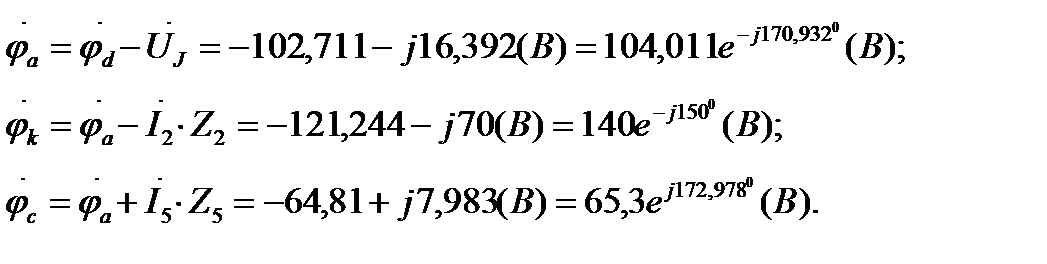
Построим топографическую диаграмму напряжений и векторную диаграмму токов (рис.8).
Рис.8 – Топографическая диаграмма напряжений и векторная диаграмма токов
3. расчёт разветвлённой электрической цепи переменного тока при периодических негармонических источниках
В заданной схеме при  действуют источники ЭДС
действуют источники ЭДС

источник тока J(t)=0.
1. Рассчитать токи от действия постоянной составляющей и первой гармоники.
2. Рассчитать составляющие третьей гармоники всех токов. Для проверки правильности расчёта составить баланс активных и реактивных мощностей.
Исходные данные:
Таблица 1
| № | Е1 | Е2 | 
| 
|
| - | В | В | град | град |
Таблица 2
| № | R | L | C |
| - | Ом | мГн | мкФ |
| 31,85 | 318,4 |
Рис.9 - Исходная схема
3.1. Расчёт электрических токов методом наложения
Воздействие е1(t) содержит постоянную составляющую (нулевую гармонику), первую и третью гармоники.
Воздействие е2(t) содержит постоянную составляющую (нулевую гармонику) и первую гармонику.
Воздействие е3(t) содержит третью гармонику.
Расчёт по каждой составляющей воздействия проведём отдельно.
1) Рассчитаем токи в ветвях схемы от действия постоянной составляющей ЭДС (нулевой гармоники):

Ей соответствует схема замещения (рис.10):
Рис. 10 - Схема для расчёта токов от действия постоянной составляющей
Расчёт произведём методом контурных токов (рис.10).
Составляем систему уравнений:

Полученные контурные уравнения запишем в матричном виде:

Решим систему из двух контурных уравнений, используя метод Крамера:
 .
.
Найдём определители системы уравнений:

Тогда:

Далее находим реальные токи в ветвях схемы с учётом контурных токов, проходящих в этих ветвях:

2) Рассчитаем токи в ветвях схемы для первой гармоники:

Ей соответствует схема замещения (рис.11):
Рис. 11 - Схема для расчёта первой гармоники
Рассчитаем без учёта М комплексные сопротивления ветвей и изобразим комплексную схему замещения (рис.12):


Рис. 12 - Комплексная схема замещения
Произведём расчёт методом контурных токов (рис.12).
В результате получим следующие уравнения для контурных токов (встречное включение):

Группируем слагаемые и записываем уравнения в матричном виде:

Решим систему из двух контурных уравнений, используя метод Крамера:

Найдём определители системы уравнений:

Тогда:

Далее находим реальные токи в ветвях схемы с учётом контурных токов, проходящих в этих ветвях:
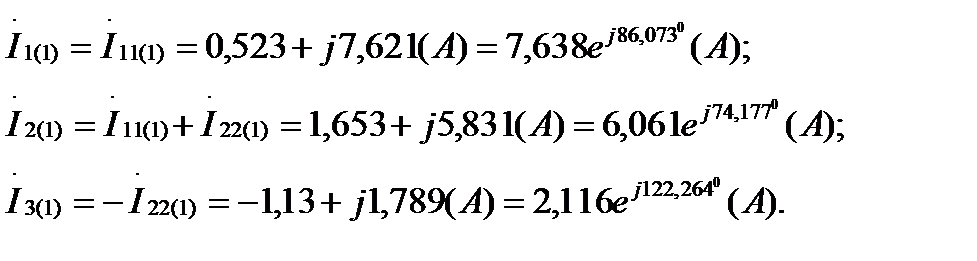
Мгновенные значения токов:

3) Рассчитаем токи в ветвях схемы для третьей гармоники (k = 3):

Ей соответствует схема замещения (рис.13):
Рис. 13 - Схема для расчёта третьей гармоники
Рассчитаем без учёта М комплексные сопротивления ветвей и изобразим комплексную схему замещения (рис.14):

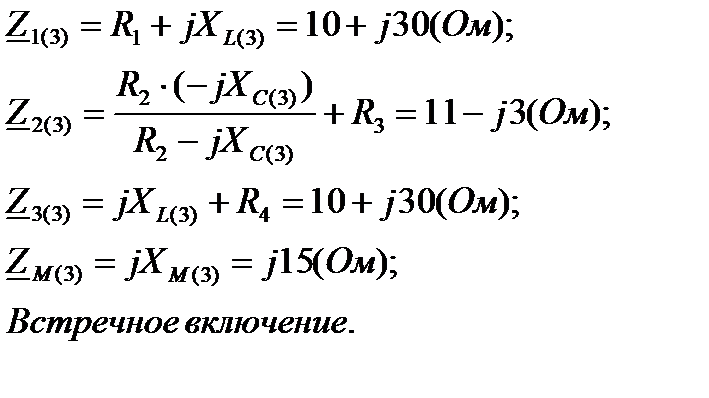
Рис.14 - Комплексная схема замещения
Произведём расчёт методом контурных токов (рис.14).
В результате получим следующие уравнения для контурных токов (встречное включение):

Группируем слагаемые и записываем уравнения в матричном виде:

Решим систему из двух контурных уравнений, используя метод Крамера:

Найдём определители системы уравнений:

Тогда:

Далее находим реальные токи в ветвях схемы с учётом контурных токов, проходящих в этих ветвях:

Мгновенные значения токов:

Результирующее действие определяем методом наложения мгновенных значений: мгновенное значение тока любой ветви равно сумме мгновенных значений отдельных гармоник:

Действующие значения токов:

Действующие значения ЭДС:

Date: 2016-11-17; view: 598; Нарушение авторских прав