
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Анализ баланса мощностей
|
|
СОДЕРЖАНИЕ
Введение........................................................................................................................................ 3
1. расчёт разветвлённой цепи постоянного тока......................................... 4
1.1. Расчёт токов методом контурных токов................................................................ 5
1.2. Анализ баланса мощностей...................................................................................... 7
1.3. Расчёт тока в ветви методом эквивалентного генератора............................... 7
2. Расчёт разветвлённой однофазной электрической цепи переменного тока 10
2.1. Расчёт параметров комплексной схемы замещения........................................ 11
2.2. Расчёт токов схемы методом контурных токов в комплексной форме....... 12
2.3. Анализ баланса активной и реактивной мощностей........................................ 14
2.4. Построение векторной диаграммы токов и напряжений.................................. 15
3. расчёт разветвлённой электрической цепи переменного тока при периодических негармонических источниках............................................... 17
3.1. Расчёт электрических токов методом наложения............................................ 18
3.2. Проверка баланса мощностей................................................................................ 25
4. Расчёт симметричной трёхфазной электрической цепи переменного тока 29
4.1. Расчёт фазных и линейных токов схемы.............................................................. 30
4.2. Анализ баланса активной и реактивной мощностей........................................ 32
4.3. Построение векторной диаграммы токов и напряжений.................................. 32
5. Расчёт динамичной трёхфазной электрической цепи переменного тока с местной несимметрией..................................................................................................... 35
5.1. Расчёт симметричных составляющих.................................................................. 36
5.2. Анализ баланса активной и реактивной мощностей........................................ 42
заключение................................................................................................................................ 44
список использованных источников.................................................................... 45
Введение
Теоретические основы электротехники (ТОЭ) – это техническая дисциплина, связанная с изучением теории электричества и электромагнетизма, являющаяся базовым общетехническим курсом для электротехнических и электроэнергетических специальностей вузов.
Цель курсовой работы – освоение расчёта и анализа цепей современными методами, приобретение навыков краткого изложения сущности производимых расчётов и анализа полученных результатов.
Для осуществления поставленной цели в рамках курсовой работы необходимо выполнить следующие задачи:
- произвести расчёт разветвлённой цепи постоянного тока;
- осуществить расчёт разветвлённой однофазной электрической цепи переменного тока;
- выполнить расчёт разветвлённой электрической цепи переменного тока при периодических негармонических источниках;
- произвести расчёт симметричной трёхфазной электрической цепи переменного тока;
- осуществить расчёт динамичной трёхфазной электрической цепи переменного тока с местной несимметрией.
Объект исследования – теоретические основы электротехники.
Предмет исследования – электромагнитные явления и процессы, происходящие в электрических цепях постоянного и переменного тока.
В качестве источников информации рассматриваются научные труды зарубежных и отечественных специалистов по теоретическим основам электротехники.
Структурно работа состоит из введения, пяти разделов, заключения, источников использованной литературы. Общий объём работы 44 страницы. Работа иллюстрирована 23 рисунками. Библиографический список включает 7 источников.
1. расчёт разветвлённой цепи постоянного тока
Для заданной схемы с постоянными во времени источниками ЭДС и тока, принимая  ,
, 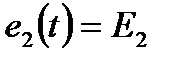 ,
,  ,
, 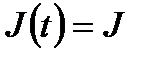 , выполнить следующее:
, выполнить следующее:
1. Изобразить схему, достаточную для расчёта токов ветвей, соединяющих узлы, помеченные буквами, указав их номера и направления.
2. Определить токи во всех ветвях схемы и напряжение на зажимах источника тока методом контурных токов.
3. Составить баланс вырабатываемой и потребляемой мощностей.
4. Рассматривая цепь относительно сопротивления R ветви ab как активный двухполюсник, заменить его эквивалентным генератором, определить параметры эквивалентного генератора и рассчитать ток в ветви ab.
Исходные данные:
Таблица 1
| № | Е1 | Е2 |
| - | В | В |
Таблица 2
| № | J | R |
| - | А | Ом |
Рис.1 - Исходная схема
1.1. Расчёт токов методом контурных токов
Изобразим схему, достаточную для расчёта токов ветвей, соединяющих узлы, помеченные буквами, указав их номера и направления (рис.2). При этом учитываем, что индуктивный элемент L для постоянного тока является «закороткой», а ёмкостный элемент C при постоянном токе представляет собой «разрыв» ветви, причём взаимная индукция M влияния на постоянные токи не оказывает. Указываем произвольно номера и направления токов в ветвях схемы.
Рис.2 - Схема для расчёта токов методом контурных токов
Определяем токи во всех ветвях схемы и напряжение на зажимах источника тока методом контурных токов.
Количество узлов в схеме: 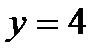 .
.
Общее число ветвей:  .
.
Число ветвей с источником тока: 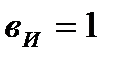 .
.
Число ветвей с неизвестными токами: 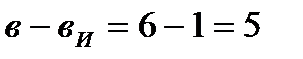 .
.
Число контуров, необходимое и достаточное для определения всех неизвестных токов:  .
.
Обозначаем на схеме контура I11 (dcad), I22 (bdcb), I33 (bcab) и выбираем направления их обхода, при этом через источник тока должен проходить один контурный ток (рис.2). Ток данного контура известен и равен току источника, т.е. 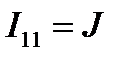 .
.
Составляем систему уравнений:
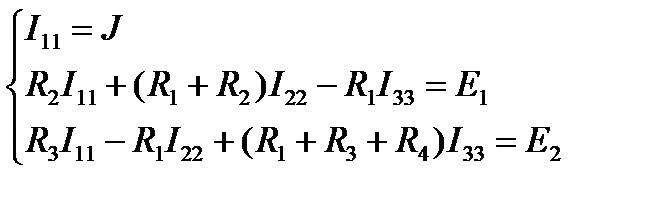 .
.
Полученные контурные уравнения запишем в матричном виде:

Решим систему из двух контурных уравнений, используя метод Крамера:
 .
.
Найдём определители системы уравнений:

Тогда:

Далее находим реальные токи в ветвях схемы с учётом контурных токов, проходящих в этих ветвях:

Напряжение на зажимах источника тока найдём при помощи второго закона Кирхгофа для контура dcad:
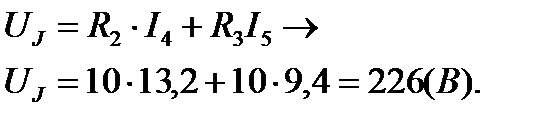
Таким образом, сущность метода контурных токов заключается в предположении, что в каждом контуре проходит свой ток (контурный ток). Тогда на общих участках, расположенных на границе двух соседних контуров, будет протекать ток, равный алгебраической сумме токов этих контуров. Уравнения составляют только по второму закону Кирхгофа, но не для действительных, а для воображаемых (контурных) токов, циркулирующих по замкнутым контурам электрической цепи.
Основное преимущество данного метода состоит в том, что он использует меньшее количество неизвестных величин и меньшее количество уравнений при анализе сложных схем.
Анализ баланса мощностей
Уравнение энергетического баланса при питании от источников ЭДС и источника тока имеет вид [1]:

где 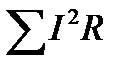 - суммарная мощность приёмников;
- суммарная мощность приёмников;
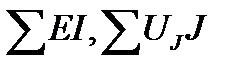 - суммарная мощность источников.
- суммарная мощность источников.
Составляем баланс вырабатываемой и потребляемой мощности:
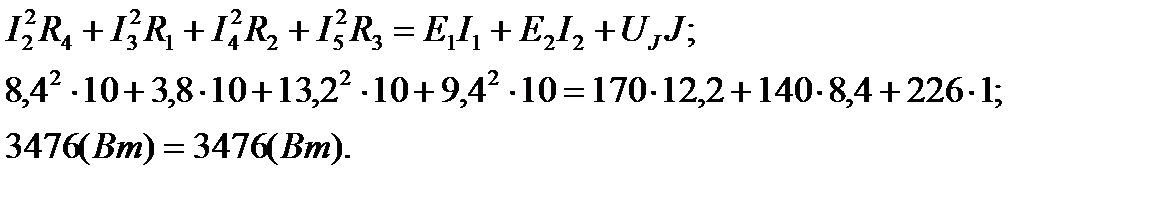
Допустимая относительная погрешность расчётов:

Как видим, баланс мощностей сходится, значит расчёт произведён верно.
1.3. Расчёт тока в ветви методом эквивалентного генератора
Определим ток в ветви ab методом эквивалентного генератора.
Найдём напряжение на зажимах разомкнутой ветви ab (рис.3).
Рис.3 - Напряжение холостого хода (эквивалентного генератора)
Напряжение на зажимах разомкнутой ветви ab:
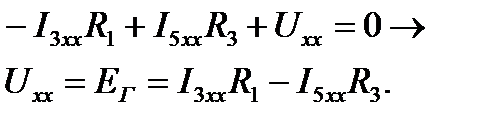
Неизвестные токи I3хх и I5хх найдём по методу контурных токов:
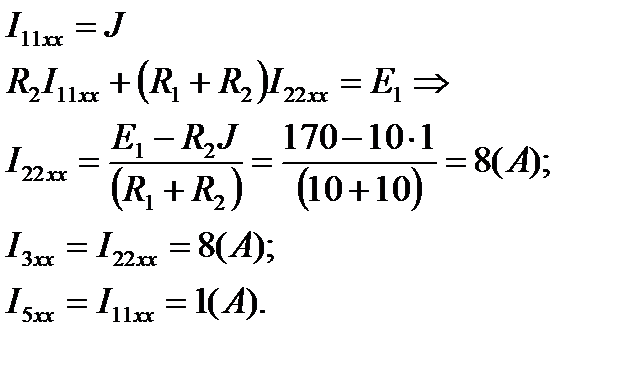
Напряжение холостого хода или ЭДС эквивалентного генератора:
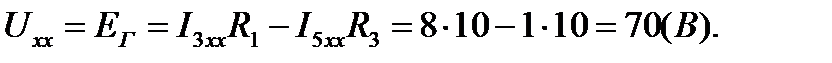
Сопротивление эквивалентного генератора (рис.4):
Рис.4 - Сопротивление эквивалентного генератора
Сопротивление эквивалентного генератора:

Ток в ветви ab:

Расчёт методом эквивалентного генератора позволяет найти ток I4, который совпадает с результатами п.1.1.
Таким образом, метод эквивалентного генератора, основанный на теореме об активном двухполюснике (называемой также теоремой Гельмгольца-Тевенена), позволяет достаточно просто определить ток в одной (представляющей интерес при анализе) ветви сложной линейной схемы, не находя токи в остальных ветвях. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны.
Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.
2. Расчёт разветвлённой однофазной электрической цепи переменного тока
Для заданной схемы с источниками гармонических ЭДС и тока

при  и
и 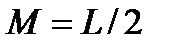 выполнить следующее.
выполнить следующее.
1. Рассчитать без учёта М комплексные сопротивления ветвей, соединяющих узлы, помеченные на схеме буквами и изобразить комплексную схему замещения с этими сопротивлениями для расчёта комплексов действующих значений токов ветвей (номера и направления токов сохранить согласно заданию №1, причём параллельное соединений R и C представить в виде одного комплексного сопротивления).
2. Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на зажимах источника тока методом контурных токов.
3. Рассчитать балансы активной и реактивной мощностей.
4. Построить лучевую диаграмму токов и совмещённую с ней топографическую диаграмму напряжений.
Исходные данные:
Таблица 1
| № | Е1 | Е2 | 
| 
|
| - | В | В | град | град |
Таблица 2
| № | J | 
| R | L | C |
| - | А | град | Ом | мГн | мкФ |
| 31,85 | 318,4 |
Рис.5 - Исходная схема
2.1. Расчёт параметров комплексной схемы замещения
Рассчитаем без учёта M комплексные сопротивления ветвей, соединяющих узлы, помеченные на схеме буквами, и изобразим комплексную схему замещения с этими сопротивлениями для расчёта комплексов действующих значений токов ветвей (параллельное соединение R и C представим в виде одного комплексного сопротивления):
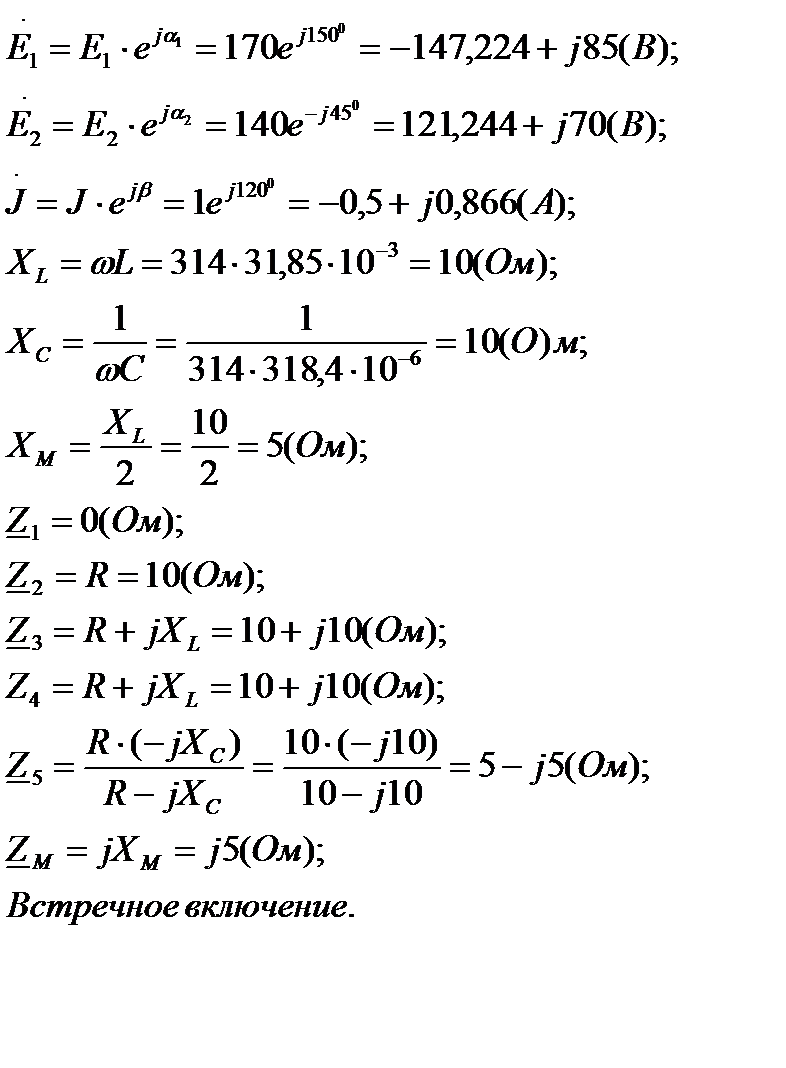
Изображаем комплексную схему замещения с сопротивлениями и комплексами действующих значений (рис.6).
Рис.6 - Комплексная схема замещения
2.2. Расчёт токов схемы методом контурных токов в комплексной форме
Не исключая индуктивной связи, определим комплексы действующих значений токов всех ветвей и напряжение на зажимах источника тока методом контурных токов.
Обозначаем на схеме контура I11 (badb), I22 (bcab), I33 (dcabd). Контурные токи направляем так, чтобы через источник тока проходил один контурный ток и через каждое индуктивно связанное сопротивление проходил один свой контурный ток (рис.7).
Рис.7 - Схема для расчёта токов методом контурных токов
В результате получим следующие уравнения для контурных токов (встречное включение):
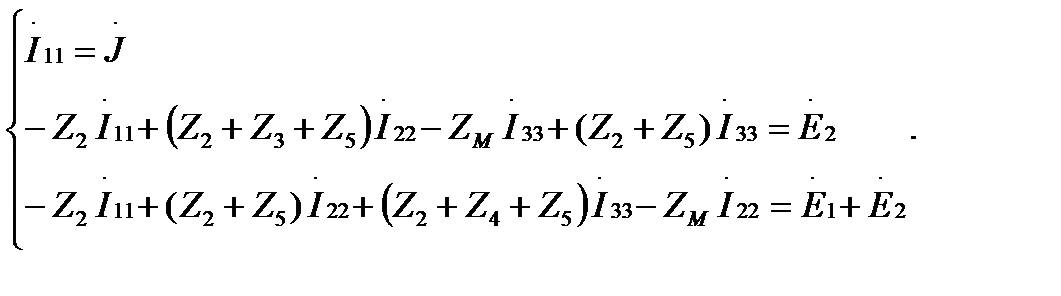
Группируем слагаемые и записываем уравнения в матричном виде:
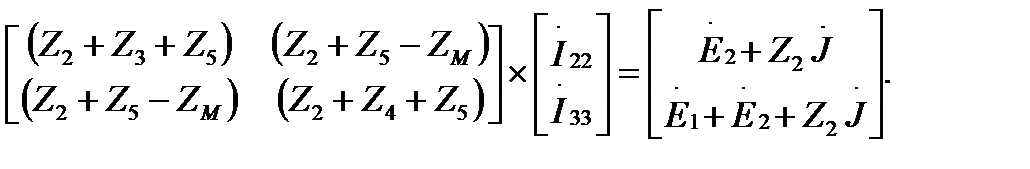
Решим систему из двух контурных уравнений, используя метод Крамера:
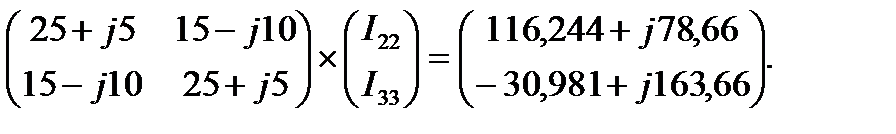
Найдём определители системы уравнений:
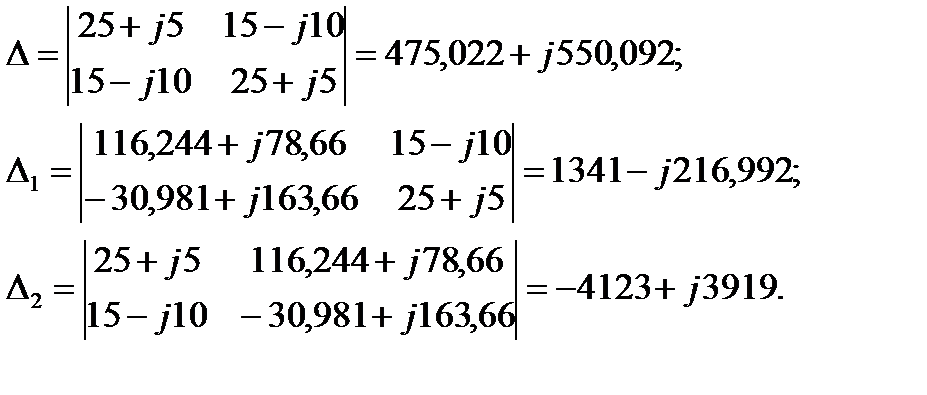
Тогда:

Далее находим реальные токи в ветвях схемы с учётом контурных токов, проходящих в этих ветвях:

Напряжение на зажимах источника тока найдём при помощи второго закона Кирхгофа для контура badb:
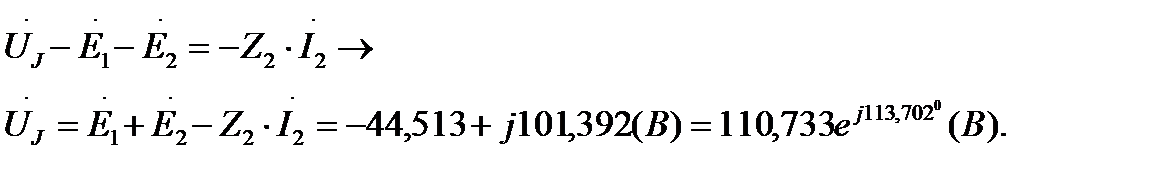
Таким образом, для расчёта линейных цепей с гармоническими токами и напряжениями применяется символический метод. Этот метод основан на изображении гармонических величин комплексными числами. Символический метод позволяет перейти от расчета линейных цепей с переменными во времени напряжениями и токами к расчёту комплексной схемы замещения с постоянными напряжениями и токами. Для комплексных схем замещения справедливы все метод расчёта, используемые при постоянных напряжениях и токах, но в комплексной форме.
Date: 2016-11-17; view: 1312; Нарушение авторских прав