Молекулярная физика и термодинамика

2.1 Основы молекулярно–кинетической теории

2.1.1 Молекулярная физика: от атома к молекуле. Масса атомов и молекул. Количество вещества. Число Авогадро

Все тела состоят из молекул, атомов и элементарных частиц, которые разделены промежутками, беспорядочно движутся и взаимодействуют друг с другом.

Согласно атомистической теории строения вещества, мельчайшей частицей вещества, сохраняющей все его химические свойства, является молекула.

Таким образом, внутри каждой песчинки и капельки существует свой микромир взаимодействующих между собой триллионов молекул. Закономерности этого мира молекул изучает молекулярная физика.

Один моль вещества содержит количество молекул или атомов, равное постоянной Авогадро.

Закон кратных отношений, открытый Дальтоном, утверждал, что, если два элемента образуют между собой несколько молекулярных соединений, то масса одного элемента, приходящаяся на одну и ту же массу другого, относятся между собой как небольшие целые числа. Например, при взаимодействии азота с кислородом образуются пять оксидов. На 1 грамм азота в образующихся молекулах приходится 0,57, 1,14, 1,71, 2,28, 2,85 грамм кислорода, что соответствует отношением 2:1, 1:1, 2:3, 1:2, 2:5 в этих оксидах, и поэтому состав молекул этих оксидов можно записать в виде N₂O, NO, N₂O₃, NO₂, N₂O₅.

Возьмём другой пример. Для образования молекулы углекислого газа требуется соединить один атом углерода с двумя атомами кислорода (CO ₂) или по весу, например, 12 г углерода и 32 г кислорода. Из 12 г углерода можно создать также газ метан (CH ₄), если они вступят в реакцию с 4 г водорода. Из этого следует, что в 1 г водорода, 12 г углерода и 16 г кислорода содержится одно и то же число атомов. Оказалось, что самыми лёгкими являются атомы водорода, поэтому массу остальных атомов сначала измеряли в единицах равных массе атома водорода. Однако сейчас за единицу массы взята 1/12 массы атома углерода, его изотопа ¹² С. Таким образом, относительной молекулярной или атомной массой вещества называют отношение массы его молекулы и атома к 1/12 массе атома углерода.

Чем больше молекул в кусочке или объёме данного вещества, тем больше вещества там содержится. Чтобы оценить, сколько находится вещества в данном его образце, число молекул в нём сравнивают с числом N _А молекул в 12 г углерода. Таким образом, к оличество вещества, n, содержащееся в некотором его кусочке или объёме, равно:

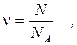(27)

где N - число молекул в данном его образце. Единицей измерения количества вещества в системе СИ служит моль – количество вещества, содержащееся в 12 г углерода. Другими словами, один моль вещества содержится в его массе, выраженной в граммах и равной относительной молекулярной (или атомной) массе этого вещества. Так, моль углерода содержится в 12 его граммах, моль кислорода (O ₂) – в 32 его граммах, и т.д.

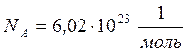
Число атомов (или молекул) в одном моле называют числом или постоянной Авогадро, N _А, измерить которую удалось только в начале XX века французскому физику Жану Перрену, и за эту работу, демонстрирующую «дискретную природу материи» в 1926 г. он был удостоен Нобелевской премии по физике. Согласно современным измерениям:

(28)

Молярной массой, M называют отношение массы m данного образца вещества к количеству n вещества, содержащегося в нём:

- которая численно равна массе вещества, взятого в количестве одного моля. Молярная масса в системе СИ выражается в кг/моль. Найдём молярную массу воды (H ₂ O). 1 моль воды содержится в её 0,018 кг, и значит, M _H2O= 0,018 кг/моль.

Абсолютное значение массы m _В атомов или молекул любого вещества можно легко вычислить, если знать молярную массу M этого вещества и постоянную Авогадро, N _А. Например, масса одной молекулы воды равна 3^.10^{-26 кг. Аналогично можно вычислить массу атома углерода, 1/12 которой приняли за атомную единицу массы (а.е.м):}

Знание числа Авогадро даёт также возможность оценить размер молекул или объём V ₀, приходящийся на одну молекулу. Пусть данное вещество имеет молярную массу M, а его образец, содержащий n молей этого вещества, имеет массу m, объём V и плотност ь, т.е. отношение массы к объёму, r. Найдём V ₀, разделив V на число молекул N в образце и используя (27) и (28):

(29)

Например, объём, приходящийся на одну молекулу воды (r = 10³ кг/м³, М =0,018 кг/моль), согласно (29), составит 3^.10^{-29 м3}. Если считать, что молекула имеет форму кубика этого объёма, то длина ребра этого кубика, или размер молекулы воды равен 3,1^.10^{-10 м.}

2.1.2 Идеальный газ: основное уравнение молекулярно-кинетической теории газов. Температура, тепловое равновесие, абсолютная температура

Давление идеального газа пропорционально произведению концентрации молекул на их среднюю кинетическую энергию.

Газ окружает нас со всех сторон. В любом месте на земле, даже под водой, мы носим на себе часть атмосферы, нижние слои которой сжимаются под действием силы тяжести верхних. Поэтому, измеряя атмосферное давление можно судить о том, что происходит высоко над нами и предсказывать погоду. Что же такое давление газа, и как крошечные молекулы воздуха его создают?

Давлением p на данном участке поверхности, называют отношение силы F, действующей перпендикулярно этой поверхности к площади S данного её участка:

(30)

Единицей измерения давления в СИ служит Паскаль (Па). 1 Па = 1 Н/м².

Чтобы объяснить, как молекулы газа могут оказывать давление на поверхности, огранивающие его объём, допустим, что расстояние между молекулами намного превышает их размеры, и поэтому молекулы не взаимодействуют между собой, а лишь время от времени сталкиваются, как упругие шарики, и при этом их общая кинетическая энергия сохраняется. Такой газ называют идеальным.

(31)

Найдём силу F, с которой действует молекула массой m ₀ на поверхность, от которой она отскакивает. При отражении от поверхности, длящемся промежуток времени D t, составляющая скорости молекулы, перпендикулярная этой поверхности, v _y изменяется на обратную (- v _y). Поэтому при отражении от поверхности молекула приобретает импульс, 2 m ₀ v _y, а значит, по третьему закону Ньютона 2 m ₀ v _y =FD t, откуда:

Формула (31) даёт возможность вычислить силу, с которой давит одна молекула газа на стенку сосуда в течение интервала D t. Чтобы определить среднюю силу давления газа, например, за одну секунду, надо найти, сколько молекул отразится за секунду от участка поверхности площадью S, а также необходимо знать среднюю величину скорости v _y молекул, движущихся в направлении к данной поверхности.

Пусть в единице объёма газа находится n молекул. Упростим себе задачу, считая, что все молекулы газа движутся с одинаковой скоростью, v. При этом 1/3 всех молекул движется вдоль оси Ox, и столько же – вдоль оси Oy и Oz. Пусть половина молекул, движущихся вдоль оси Oy, движется в сторону стенки С, а остальные – в противоположную сторону. Тогда, очевидно, количество молекул в единице объёма, несущихся в сторону стенки С, составит n /6.

Найдём теперь количество молекул, ударившихся об участок поверхности площадью S за одну секунду. Очевидно, что за 1 с до стенки успеют долететь те молекулы, которые движутся в её сторону и находятся на расстоянии, не большем v. Поэтому ударятся об этот участок поверхности 1/6 всех молекул, находящихся в прямоугольном параллелепипеде, длина которого равна v, а площадь торцевых граней - S. Так как объём этого параллелепипеда составляет Sv, то общее число N молекул, ударившихся об участок поверхности стенки за 1 с будет равно:

(32)

Используя (31) и (32) можно вычислить импульс, который за 1 с сообщил молекулам газа участок поверхности стенки площадью S. Этот импульс численно будет равен силе давления газа, F:

откуда, используя (30), получаем следующее выражение, связывающее давление газа и среднюю кинетическую энергию поступательного движения его молекул:

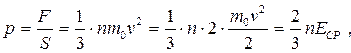(33)

где Е _СР – средняя кинетическая энергия молекул идеального газа. Формулу (33) называют основным уравнением молекулярно-кинетической теории газов.

Тепловое равновесие между телами возможно только тогда, когда их температура одинакова.

Прикоснувшись рукой к любому предмету, мы легко можем определить, тёплый он или холодный. Если температура предмета ниже температуры руки, предмет кажется холодным, а если наоборот, то - тёплым. Если зажать в кулаке холодную монету, то теплота руки начнёт нагревать монету, и через некоторое время её температура станет равной температуре руки, или, как говорят, наступит тепловое равновесие. Поэтому температура характеризует состояние теплового равновесия системы из двух или нескольких тел, имеющих одну и ту же температуру. Так, говоря, что температура нашего тела равна 36 ^о С, мы подразумеваем, что градусник подмышкой находится в тепловом равновесии с окружающими тканями, когда он показывает 36 ^о С.

Температура наряду с объёмом и давлением газа являются макроскопическими параметрами. Для измерения температуры используют термометры. В некоторых из них регистрируют изменение объёма жидкости при нагревании, в других – изменение электрического сопротивления и т.п. Самой распространённой является температурная шкала Цельсия, названная так в честь шведского физика А. Цельсия. Чтобы получить температурную шкалу Цельсия для жидкостного термометра, его сначала погружают в тающий лёд и отмечают положение конца столбика, а потом - в кипящую воду. Отрезок между этими двумя положениями столбика делят на 100 равных частей, считая, что температура таяния льда соответствует нулю градусов шкалы Цельсия (^о С), а температура кипящей воды – 100 ^о С (см. рис. 6 а).

Основное уравнение молекулярно-кинетической теории (33) связывает между собой давление газа, концентрацию молекул и их среднюю кинетическую энергию. Однако средняя кинетическая энергия молекул, как правило, неизвестна, хотя результаты многих опытов говорят о том, что скорость молекул увеличивается с ростом температуры Зависимость средней кинетической энергии молекул газа от его температуры можно получить из закона открытого французским физиком Ж. Шарлем в 1787 году.

Согласно закону Шарля, если объём данной массы газа не меняется, его давление p _t линейно зависит от температуры t:

(34)

где t – температура газа, измеренная в ^о С, а p ₀ – давление газа при температуре 0 ^о С (см. рис. 6 б). Таким образом, из закона Шарля следует, что давление газа, занимающего неизменный объём, пропорционально сумме (t +273 ^о С). С другой стороны, из (33) вытекает, что, если концентрация молекул постоянна, т.е. объём, занимаемый газом, не изменяется, то давление газа должно быть пропорционально средней кинетической энергии молекул. Значит, средняя кинетическая энергия, Е _СР молекул газа, просто, пропорциональна величине (t +273 ^о С):

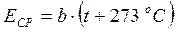(35)

где b – постоянный коэффициент, значение которого мы позже определим. Из (35) следует, что средняя кинетическая энергия молекул станет равной нулю при -273 ^о С. Исходя из этого, английский учёный У. Кельвин в 1848 г. предложил использовать абсолютную температурную шкалу, нулевая температура в которой соответствовала бы -273 ^о С, а каждый градус температуры был бы равен градусу шкалы Цельсия. Таким образом, абсолютная температура, T связана с температурой t, измеренной по шкале Цельсия, следующим образом:

(36)

За единицу абсолютной температуры в СИ принят Кельвин (К).

(37)

Учитывая (36), уравнение (35) преобразуется в:

(38)

подставляя которое в (33), получаем следующее:

(39)

(40)

Чтобы избавиться от дроби в (38), заменим 2 b /3 на k, и получим вместо (37) и (38) два очень важных уравнения:

где k – постоянная Больцмана, названная в честь Л. Больцмана. Эксперименты показали, что k =1,38.10^-23 Дж/К. Таким образом, давление газа и средняя кинетическая энергия его молекул пропорциональны его абсолютной температуре.

Рисунок 6 (а) – Градуировка термометра по шкале Цельсия;

(б) – Графическое представление закона Шарля.

2.1.3 Уравнение состояния идеального газа. Закон Авогадро. Изопроцессы в газах: газовые законы

Уравнение состояния идеального газа связывает между собой три его макроскопические характеристики – занимаемый газом объём, его давление и температуру.

Мы вывели формулу, связывающую давление идеального газа, p, концентрацию молекул в нём, n, и его абсолютную температуру, Т:

p = nkT, (41)

где k – постоянная Больцмана. Однако в большинстве случаев пользоваться формулой (41) неудобно, т.к. величина n, как правило, неизвестна, а мы лишь знаем, какой это газ и какой объём он занимает. Чтобы в этих случаях формулой (41) было пользоваться проще, преобразуем её следующим образом. Пусть газ, состоящий из N молекул, находится в сосуде объёмом V. Тогда концентрация, n молекул равна:

(42)

где m и n - масса и количество вещества, содержащееся в газе с молярной массой M и объёмом V, а N _A – число Авогадро. Подставляя (42) в (41), получаем:

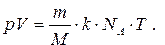(43)

Произведение kN _A обозначают буквой R и называют универсальной (молярной) газовой постоянной, которая равна 8,31 Дж/(моль^.К). Заменяя kN _A на R в формуле (43), получаем:

(44)

Уравнение (44) называют уравнением состояния идеального газа или уравнением Менделеева-Клапейрона, названным в честь русского учёного Д.И. Менделеева и французского физика Б. Клапейрона. Формула (44) определяет взаимозависимость трёх макроскопических характеристик данной массы газа, определяющих его состояние, – давления, объёма и температуры.

Уравнение Менделеева-Клапейрона позволяет вычислить одну из пяти переменных (p, V, m, M и T), если значения остальных четырёх известны. Можно, например, найти молярную массу, М газа, т.е. определить его относительную молекулярную массу, если измерить его давление, объём, массу и температуру.

Из уравнения (44) следует, что если данная масса газа находится в состоянии 1, в котором её давление, объём и температуры равны p ₁, V ₁ и T ₁, соответственно, а потом переходит в состояние 2 (см. рис. 7 а), в котором её давление, объём и температуры становятся равными p ₂, V ₂ и T ₂, то:

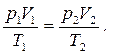(45)

Уравнение (45), называемое уравнением Клапейрона, позволяет вычислить значение одной из макроскопических характеристик газа в состоянии 2, если остальные две известны.

Возьмём одинаковое число молей n двух разных газов (А и Б). Пусть эти газы имеют одинаковую температуру T ₀ и давление p ₀. Тогда из уравнения (44) следует, что объёмы этих газов, V _А и V _Б, тоже равны:

(46)

Таким образом, при одинаковых давлении и температуре равные объёмы различных газов содержат одинаковое количество вещества, т.е. молекул. Этот вывод называют законом Авогадро. Из закона Авогадро и формулы (46) следует, что при нормальных условиях, т.е. при температуре 0^о С (Т ₀=273 К) и нормальном атмосферном давлении (p ₀=101325 Па), газ, взятый в количестве 1 моль, занимает объём 0,0224 м³ или 22,4 литра (см. рис. 7 б).

Рисунок 7 (а) – Связь между параметрами газа в двух его состояниях; (б) – Связь между параметрами одного моля газа при нормальных условиях.

Из уравнения Менделеева - Клапейрона следуют законы, по которым изменяется состояние газов, когда один из параметров – температура, давление или объём остаются неизменным.

В большинстве случаев при переходе газа из одного состояния в другое меняются все его параметры – температура, объём и давление. Так происходит, когда газ сжимается под поршнем в цилиндре двигателя внутреннего сгорания, в результате чего температура газа и его давление растут, а объём уменьшается. Однако в некоторых случаях изменения одного из параметров газа относительно малы или вообще отсутствуют. Такие процессы, где один из трёх параметров – температура, давление или объём остаются неизменными, называют изопроцессами, а законы, которые их описывают – газовыми законами.

Изотермическим процессом называют изменение состояния газа, при котором его температура остаётся постоянной. Примером такого процесса может служить накачивание воздухом автомобильных шин. Однако изотермическим такой процесс можно считать, если сравнивать состояние воздуха перед тем, как он оказался в насосе, с его состоянием в шине после того, как температура шины и окружающего воздуха стали равными. Любые медленные процессы, происходящие с малым объёмом газа, окружённым большой массой газа, жидкости или твёрдого тела, имеющей постоянную температуру, можно считать изотермическими.

Из уравнения состояния идеального газа (44) следует, что при изотермическом процессе произведение давления данной массы газа на его объём есть величина постоянная. Этот закон, называемый законом Бойля-Мариотта, был открыт английским учёным Р. Бойлем и французским физиком Э. Мариоттом и записывается в следующем виде:

(47)

График, иллюстрирующий, как изменяется давление газа в зависимости от его объёма при изотермическом процессе, называют изотермой и имеет вид гиперболы (см. рис. 8 а). Видно, что расширение газа при изотермическом процессе сопровождается падением его давления.

Изобарным процессом называют изменение состояния газа, происходящее при постоянном давлении. Согласно уравнению Менделеева-Клапейрона (44) при изобарном процессе отношение объёма данной массы газа к его температуре постоянно. Этот вывод, который называют законом Гей-Люссака в честь французского учёного Ж. Гей-Люссака, можно записать в виде:

(48)

График, показывающий, как объём газа зависит от его температуры при изобарическом процессе, называют изобарой, которая, как видно на рис. 8 б, является прямой, проходящей через начало координат. На самом деле, при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому изобары на рис. 8 б вблизи начала координат показаны пунктиром.

Процесс, при котором изменяется состояние газа, а его объём остаётся неизменным, называют изохорным. Из уравнения Менделеева-Клапейрона следует, что у газа, занимающего постоянный объём, отношение его давления к температуре тоже должно быть постоянным:

(49)

Уравнение (49) описывает закон Шарля, с которым мы уже встречались ранее. Зависимость между давлением и температурой газа при изохорном процессе называют изохорой, которая является прямой (см. рис. 8 в).

Рисунок 8 а, б, в – Изотермы, изобары и изохоры идеального газа, соответственно.

Date: 2016-08-31; view: 451; Нарушение авторских прав