Использовали правила действий над алгебраическими дробями и формулы сокращенного умножения

Пример 2.

Упростить выражение:

.

Решение:

,

если а³0, b³0, а¹b.

Использовали формулы сокращенного умножения, правила сложения дробей и умножения иррациональных выражений, тождество , определение модуля числа, понятие области допустимых значений переменных в выражении.

Пример 3.

Сократите дробь:

.

Решение:

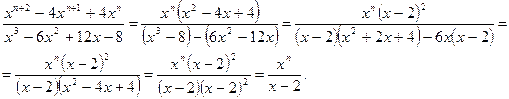
При выполнении преобразования использовали вынесение общего множителя за скобку, переместительный и сократительный законы, 2 формулы сокращенного умножения, действия над степенями.

Рекомендуемая литература.

1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия.

Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас-

сы. — М.: Просвещение, 2015. (Гриф Минобразования и науки РФ).

2. Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. пособие

для студ. учреждений сред. проф. образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

3. Богомолов Н.В. Сборник дидактических заданий по математике: учеб.пособие для ссузов / М.: Дрофа, 2012. (Гриф Минобразования и науки РФ).

4. Богомолов Н.В. Практические занятия по математике. Учебное пособие для СПО. – М.: Юрайт, 2015.

5. ЕГЭ по математике: подготовка к тестированию

http://www.uztest.ru

6. Информационные, тренировочные и контрольные материалы

www. fcior.edu. ru

Критерии оценки:

• ознакомление с условием задачи (анализ условия задачи и его наглядная интерпретация схемой или чертежом), 0,5 балла;

• составление плана решения задачи (составление уравнений, связывающих величины, которые характеризуют рассматриваемое явление с количественной стороны), 1 балл;

• подробное решение, 2 балла;

• проверка правильности решения (анализ полученного результата или числовой расчет), ответы на контрольные вопросы 1 балл;

• задача представлена на контроль в срок, 0,5 балла.

Максимальное количество баллов: 5

Оценка выставляется по количеству набранных баллов.

3. Тема 2.2.4 « Логарифмирование и потенцирование выражений»

Форма предоставления изученного материала (по программе самостоятельного изучения с указанием уровней сложности):

1. Решение 3-4 задач.

2. Решение 5-6 задач. Ответы на контрольные вопросы.

3. Решение 7-8 задач. Проверка правильности решения. Ответы на контрольные вопросы.

Контрольные вопросы:

1. Дать определение логарифма.

2. Перечислить основные свойства логарифма.

3. Что такое логарифмирование и потенцирование?

Упражнения:

Вместо N необходимо подставить номер своего варианта.

Прологарифмировать выражения по основанию 10, 7, e:

1.

2.

3.

4.

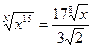
По данному логарифму найти выражение:

5.

6.

7.

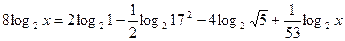
8.

Методические указания:

Логарифмирование – это нахождение логарифмов заданных чисел или выражений.

Потенцирование – это нахождение чисел или выражений по данному логарифму числа (выражения). Потенцировать – значит освобождаться от значков логарифмов в процессе решения логарифмического выражения.

При логарифмировании или потенцировании обязательно надо знать и применять свойства логарифмов.

Примеры выполнения упражнений:

Пример 1.

Найдем логарифм

Решение:

Последовательно воспользуемся сразу всеми тремя основными свойствами логарифмов (логарифм произведения, логарифм частного и логарифм степени):

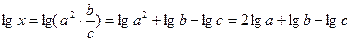
Пример 2.

По данному логарифму найти выражение:

Решение:

Используя теоремы о логарифме степени и корня, можно записать:

Затем, используя свойства степеней, получаем:

Теперь, используя теоремы о логарифме произведения и частного, получим:

Но если логарифмы двух положительных чисел по одному и тому же основанию равны, то равны и сами эти числа. Поэтому

Рекомендуемая литература.

1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия.

Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас-

сы. — М.: Просвещение, 2015. (Гриф Минобразования и науки РФ).

2. Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. пособие

для студ. учреждений сред. проф. образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

3. Башмаков М.И. Математика. Задачник: учеб. пособие для студ. учреждений сред. проф.

образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

4. Богомолов Н.В., Самойленко П.И. Математика:учебник для ссузов. – М.: Дрофа, 2012. (Гриф ФИРО)

5. Богомолов Н.В. Математика. Учебник для СПО. – М.: Юрайт, 2015.

6. Образовательный математический сайт Exponenta.ru

http://www.exponenta.ru

Критерии оценки:

• ознакомление с условием задачи (анализ условия задачи и его наглядная интерпретация схемой или чертежом), 0,5 балла;

• составление плана решения задачи (составление уравнений, связывающих величины, которые характеризуют рассматриваемое явление с количественной стороны), 1 балл;

• подробное решение, 2 балла;

• проверка правильности решения (анализ полученного результата или числовой расчет), ответы на контрольные вопросы 1 балл;

• задача представлена на контроль в срок, 0,5 балла.

Максимальное количество баллов: 5

Оценка выставляется по количеству набранных баллов.

4. Тема 2.3.1 «Преобразование алгебраических выражений. Показательные уравнения»

Форма предоставления изученного материала (по программе самостоятельного изучения с указанием уровней сложности):

1. Решение 3-4 задач.

2. Решение 5-6 задач. Ответы на контрольные вопросы.

3. Решение 7-8 задач. Проверка правильности решения. Ответы на контрольные вопросы.

Контрольные вопросы:

1. Что значит преобразовать алгебраическое выражение?

2. Какое уравнение называется показательным?

3. Перечислить способы решения показательных уравнений.

Упражнения:

Найти значение выражения:

1.

2.

3.Найти Х из равенства:

Решить уравнения:

4.

5.

6.

7.

8.

Методические указания:

1) Алгебраическим выражением называется выражение, в котором числа и буквы соединены действиями сложения, вычитания, умножения, деления, возведения в степень или извлечения арифметического корня.

При выполнении тождественных преобразований алгебраических выражений необходимо знать порядок выполнения действий, действия с дробями и степенными выражениями, формулы сокращенного умножения и др.

Следует иметь в виду, что при тождественных преобразованиях остаются неизменными:

- величина допустимых изменений буквенных величин;

- область допустимых значений каждой из буквенных величин.

Первое из этих требований является обязательным при всех преобразованиях, имеющих целью упрощение выражения или приведение его к нужному виду.

Второе требование – неизменность областей допустимых значений, не всегда выполняется при обычно применяемых нами преобразованиях. Однако это не значит, что мы должны отказываться от таких преобразований, которые изменяют области допустимых значений величин. Напротив, мы ими часто пользуемся и при упрощении выражений и при решении уравнений. Нужно только при каждом таком преобразовании указать, как изменились области допустимых значений буквенных величин.

2) Порядок выполнения действий:

- действия с одночленами;

- действия в скобках;

- умножение или деление (в порядке появления);

- сложение или вычитание (в порядке появления).

3) Напомним, что показательная функция определена лишь при a > ≠ 0, 1.

Уравнения, содержащие показательные функции, обычно приводятся к одному основанию. При решении показательных уравнений стремимся:

a. Во-первых, к получению одного основания для всех показательных функций.

b. Во-вторых, к получению одинаковых показателей для всех показательных функций.

c. Если это удастся, то делаем замену переменной и получаем более простое уравнение.

d. Если нет – попробуем уменьшить число показателей до двух и получить одинаковый суммарный показатель степени во всех слагаемых (такие уравнения называются однородными). В этом случае делим уравнение на одно из слагаемых

Примеры выполнения упражнений:

Пример 1.

Найти значение выражения:

Решение:

1. Определить порядок действий.

2. Решить пример по действиям:

1)

2)

3)

4)

5)

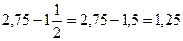
6)

7)

8)

Пример 2.

Решить уравнение:

Решение: Так как , а , то уравнение можно записать в виде

Отсюда следует, что .

Проверка подтверждает правильность решения.

Пример 3.

Решить уравнение:

Решение: Сделаем замену .

Тогда получаем квадратное уравнение: .

Решая его, находим корни: .

Откуда:

1)

2) . Уравнение не имеет решений, так как показательная функция не может быть отрицательной.

Проверка подтверждает правильность решения.

Рекомендуемая литература.

1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия.

Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас-

сы. — М.: Просвещение, 2015. (Гриф Минобразования и науки РФ).

2. Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. пособие

для студ. учреждений сред. проф. образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

3. Башмаков М.И. Математика. Задачник: учеб. пособие для студ. учреждений сред. проф.

образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

4. Богомолов Н.В., Самойленко П.И. Математика:учебник для ссузов. – М.: Дрофа, 2012. (Гриф ФИРО)

5. Богомолов Н.В. Математика. Учебник для СПО. – М.: Юрайт, 2015.

6. Научно-образовательный сайт EqWorld – Мир математических уравнений

http://eqworld.ipmnet.ru

Критерии оценки:

• ознакомление с условием задачи (анализ условия задачи и его наглядная интерпретация схемой или чертежом), 0,5 балла;

• составление плана решения задачи (составление уравнений, связывающих величины, которые характеризуют рассматриваемое явление с количественной стороны), 1 балл;

• подробное решение, 2 балла;

• проверка правильности решения (анализ полученного результата или числовой расчет), ответы на контрольные вопросы 1 балл;

• задача представлена на контроль в срок, 0,5 балла.

Максимальное количество баллов: 5

Оценка выставляется по количеству набранных баллов.

5. Тема 2.3.2 «Логарифмические уравнения и их решение»

Форма предоставления изученного материала (по программе самостоятельного изучения с указанием уровней сложности):

1. Решение 3-4 задач.

2. Решение 5-6 задач. Ответы на контрольные вопросы.

3. Решение 7-8 задач. Проверка правильности решения. Ответы на контрольные вопросы.

Контрольные вопросы:

1. Какое уравнение называется логарифмическим?

2. Перечислить способы решения логарифмических уравнений.

3. Почему при решении логарифмических уравнений необходимо находить ОДЗ?

Упражнения:

Решить логарифмические уравнения:

1.

2.

3.

4.

5.

6.

7.

8.

Методические указания:

При решении логарифмических уравнений необходимо помнить, что логарифмы обладают свойствами:

1) Логарифмы отрицательных чисел на существуют (положительное число в любой степени есть число положительное).

2) Логарифм единицы при любом основании равен нулю, , т.к .

3) Логарифм самого основания равен 1, то есть , т.к.

4) Логарифм произведения при любом основании равен сумме логарифмов сомножителей при этом же основании.

5) Логарифм дроби при любом основании равен разности логарифма числителя и логарифма знаменателя при этом же основании

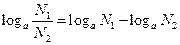
6) Логарифмом степени при любом основании равен произведению показателя степени на логарифм основания степени.

ВАЖНО!!! При решении логарифмических уравнений надо делать проверку или находить ОДЗ.

Примеры выполнения упражнений:

Пример 1.

Решение:

По определению логарифма можно записать,

надо помнить, что логарифма отрицательных чисел не существует. Так как всегда, то полученные значения оба являются корнями уравнения. Ответ:

Пример 2.

Решение: Используя определение логарифма, можно число 2 записать и тогда имеем равносильное уравнение 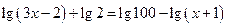. Применим свойства логарифмов и тогда

отсюда следует, что

решаем уравнение при

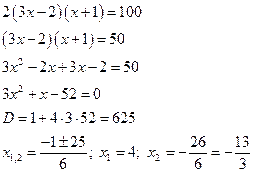
потенцирование выражений может привести к появлению посторонних корней, поэтому полученные корни нужно проверить.

Проверка:

верно.

– посторонний корень, так как логарифма отрицательных чисел не существует.

Ответ: .

Можно указать другой метод нахождения корней уравнения, основанный на предварительном нахождении всех значений x, для которых имеет смысл уравнение, то есть указать область допустимых значений переменной (ОДЗ).

По свойству логарифмов:

и тогда можно сказать, что ОДЗ удовлетворяет корень x = 4. Проверив этот корень, получаем верное равенство.

Замечание. Пользоваться указанием ОДЗ удобно для более простых выражений, стоящих под знаком логарифма.

Пример 3.

Решение:

Приведём логарифмы к одинаковому основанию. Известно, что и тогда

ОДЗ:

Пусть

И тогда ;

Если , то

Ответ:

Рекомендуемая литература.

1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия.

Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас-

сы. — М.: Просвещение, 2015. (Гриф Минобразования и науки РФ).

2. Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. пособие

для студ. учреждений сред. проф. образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

3. Башмаков М.И. Математика. Задачник: учеб. пособие для студ. учреждений сред. проф.

образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

4. Богомолов Н.В., Самойленко П.И. Математика:учебник для ссузов. – М.: Дрофа, 2012. (Гриф ФИРО)

5. Богомолов Н.В. Математика. Учебник для СПО. – М.: Юрайт, 2015.

6. Научно-образовательный сайт EqWorld – Мир математических уравнений

http://eqworld.ipmnet.ru

Критерии оценки:

• ознакомление с условием задачи (анализ условия задачи и его наглядная интерпретация схемой или чертежом), 0,5 балла;

• составление плана решения задачи (составление уравнений, связывающих величины, которые характеризуют рассматриваемое явление с количественной стороны), 1 балл;

• подробное решение, 2 балла;

• проверка правильности решения (анализ полученного результата или числовой расчет), ответы на контрольные вопросы 1 балл;

• задача представлена на контроль в срок, 0,5 балла.

Максимальное количество баллов: 5

Оценка выставляется по количеству набранных баллов.

6. Тема 4.2.3 «Скалярное произведение векторов. Действия с векторами. Использование координат и векторов при решении прикладных задач»

Форма предоставления изученного материала (по программе самостоятельного изучения с указанием уровней сложности):

1. Решение 3-4 задач.

2. Решение 5-6 задач. Ответы на контрольные вопросы.

3. Решение 7-8 задач. Проверка правильности решения. Ответы на контрольные вопросы.

Контрольные вопросы:

1.Дать определение коллинеарных векторов.

2. Сформировать правило сложения векторов, заданных своими координатами, и записать формулу.

3. Написать формулу длины вектора.

4. Дать определение скалярного произведения двух ненулевых векторов.

5. Написать формулу для вычисления скалярного произведения через координаты векторов в пространстве.

6. Сформировать необходимое и достаточное условие перпендикулярности двух ненулевых векторов

7. В чем физический смысл скалярного произведения?

8. Дать название и написать формулы законов скалярного умножения двух ненулевых векторов.

Упражнения:

1. Найдите координаты вершины D параллелограмма ABCD, если координаты трех его вершин известны:

2. Докажите, что середина отрезка с концами в точках и лежит на оси y.

3. Докажите, что середина отрезка с концами в точках и лежит на плоскости xy.

4. Даны точки (1, 2, 3), (0, -1, 2), (1, 0, -3). Найдите точки, симметричные данным относительно координатных плоскостей.

5. Даны точки (1, 2, 3), (0, -1, 2), (1, 0, -3). Найдите точки, симметричные данным относительно начала координат.

6. Даны четыре точки: Укажите среди векторов равные векторы.

7. Даны три точки: 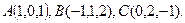Найдите точку , если известно, что векторы и равны.

8. Дано . Найти ab, если угол между векторами a и b равен 90⁰, 120⁰, 180⁰.

9. Дано и . Найти ab.

10. Дано и . Найти .

Методические указания:

1) При решении упражнений необходимо определить, какие свойства и формулы надо использовать.

Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.

× = ï ïï ïcosj

Свойства скалярного произведения:

1) × = ï ï²;

2) × = 0, если ^ или = 0 или = 0.

3) × = × ;

4) ×( + ) = × + × ;

5) (m )× = ×(m ) = m( × );

Если рассматривать векторы в декартовой прямоугольной системе координат, то

× = x_a x_b + y_a y_b + z_a z_b;

Используя полученные равенства, получаем формулу для вычисления угла между векторами:

;

2) Используя нужные формулы, решить задачу.

Примеры выполнения упражнений:

Пример 1.

Найти скалярное произведение (3 - 2 )×(5 - 6 ), если

Решение:

15 × - 18 × - 10 × + 12 × = 15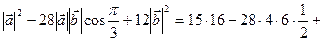

+ 12×36 = 240 – 336 + 432 = 672 – 336 = 336.

Пример 2.

Найти угол между векторами и , если

.

Решение:

Т.к. = (3, 4, 5), = (4, 5, -3), то

× = 12 + 20 - 15 =17:

.

cosj =

Пример 3.

При каком m векторы и перпендикулярны.

Решение:

= (m, 1, 0); = (3, -3, -4)

.

Пример 4.

Найти скалярное произведение векторов и , если

Решение:

()() =

= 10 +

+ 27 + 51 + 135 + 72 + 252 = 547.

Рекомендуемая литература.

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М.: Просвещение, 2014. (Гриф Минобразования и науки РФ).

2. Башмаков М.И. Математика: учебник для студ. учреждений сред. проф. образования. —

М.: Академия, 2014. (Гриф Минобразования и науки РФ).

3. Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. пособие

для студ. учреждений сред. проф. образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

4. Богомолов Н.В. Сборник дидактических заданий по математике: учеб.пособие для ссузов / М.: Дрофа, 2012. (Гриф Минобразования и науки РФ).

5. Гусев В.А., Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля: учебник для студ. учреждений сред. проф. образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

6. ЕГЭ по математике: подготовка к тестированию

http://www.uztest.ru

7. Математические этюды: 3D-графика, анимация и визуализация математических сюжетов

http://www.etudes.ru

8. Портал Allmath.ru — Вся математика в одном месте

http://www.allmath.ru

Критерии оценки:

• ознакомление с условием задачи (анализ условия задачи и его наглядная интерпретация схемой или чертежом), 0,5 балла;

• составление плана решения задачи (составление уравнений, связывающих величины, которые характеризуют рассматриваемое явление с количественной стороны), 1 балл;

• подробное решение, 2 балла;

• проверка правильности решения (анализ полученного результата или числовой расчет), ответы на контрольные вопросы 1 балл;

• задача представлена на контроль в срок, 0,5 балла.

Максимальное количество баллов: 5

Оценка выставляется по количеству набранных баллов.

7. Тема 5.2.4 «Решение тригонометрических уравнений»

Форма предоставления изученного материала (по программе самостоятельного изучения с указанием уровней сложности):

1. Решение 3-4 задач.

2. Решение 5-6 задач. Ответы на контрольные вопросы.

3. Решение 7-8 задач. Проверка правильности решения. Ответы на контрольные вопросы.

Контрольные вопросы:

1. Решение простейших тригонометрических уравнений .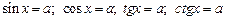

2. Частные случаи решения уравнений при ().

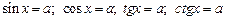3. Алгоритм решения уравнений, приводимых к одному углу и одинаковой функции.

4. Алгоритм решения уравнений, левая часть которых разлагается на множители, а правая равна нулю.

5. Решение однородных тригонометрических уравнений.

6. Решение уравнения вида .

Упражнения:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Методические указания:

1. При решении тригонометрических уравнений наиболее применимы два метода:

a) привести тригонометрическое уравнение к алгебраическому различными методами, в зависимости от условия.

b) метод разложения на множители, это общий метод решения многих уравнений. Суть его в том, что перенеся все члены в одну часть, надо постараться разложить её на множители. Таким образом, решение уравнения сводится к решению совокупности простейших уравнений.

2. Привести заданное уравнение к простейшему тригонометрическому, решить его и записать ответ.

Примеры выполнения упражнений:

Пример 1.

Решение:

Уравнение содержит функции одинакового угла, можно привести к квадратному уравнению, если заменить :

Пусть , тогда

и тогда имеем два простейших уравнения и

решаем их, применяя формулу решения уравнения

И тогда, ответ:

Пример 2.

Решение:

Замечаем, что левая часть уравнения есть однородный многочлен относительно функци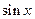й и , а правая часть равна нулю.

Такие уравнения называются однородными тригонометрическими уравнениями. Для их решения надо каждый член уравнения разделить на или 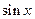в той степени, какова степень уравнения:

решаем квадратное уравнение относительно функции .

Пусть , тогда

тогда

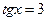
Ответ: , .

Пример 3.

Решение:

Проверим условие 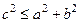; действительно 25 < 64 + 9 уравнение имеет решение.

Первый способ.

имеем:

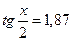и

Ответ: ; .

Второй способ.

– уравнение имеет решения

Найдем

Разделим каждый член уравнения на

Заметим, что и , а вот .

Из этого следует, что 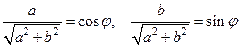, где – вспомогательный угол. Для нашего уравнения ; отсюда .

Наше уравнение принимает вид:

левая часть уравнения – это 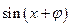и значит получаем

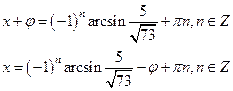
Найдем углы

Если дать значения , то получим те же углы, что и в первом случае.

Ваше желание, какому способу отдать предпочтение.

Решим ещё: 2) проверим условие:

– частный случай

Пример 4.

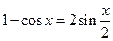
Решение:

Левая часть уравнения это формула

Ответ: .

Пример 5.

Решение:

Применим формулу к левой части уравнения:

Ответ: .

Рекомендуемая литература.

1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия.

Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас-

сы. — М.: Просвещение, 2015. (Гриф Минобразования и науки РФ).

2. Башмаков М.И. Математика: учебник для студ. учреждений сред. проф. образования. —

М.: Академия, 2014. (Гриф Минобразования и науки РФ).

3. Богомолов Н.В. Математика. Учебник для СПО. – М.: Юрайт, 2015.

4. Богомолов Н.В. Практические занятия по математике. Учебное пособие для СПО. – М.: Юрайт, 2015.

5. Никольский С.М. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. — М.: Просвещение, 2015. (Гриф Минобразования и науки РФ).

6. Научно-образовательный сайт EqWorld – Мир математических уравнений

http://eqworld.ipmnet.ru

Критерии оценки:

• ознакомление с условием задачи (анализ условия задачи и его наглядная интерпретация схемой или чертежом), 0,5 балла;

• составление плана решения задачи (составление уравнений, связывающих величины, которые характеризуют рассматриваемое явление с количественной стороны), 1 балл;

• подробное решение, 2 балла;

• проверка правильности решения (анализ полученного результата или числовой расчет), ответы на контрольные вопросы 1 балл;

• задача представлена на контроль в срок, 0,5 балла.

Максимальное количество баллов: 5

Оценка выставляется по количеству набранных баллов.

Семестр

8. Тема 7.2.2 «Параллелепипед, его виды, свойства»

Форма предоставления изученного материала (по программе самостоятельного изучения с указанием уровней сложности):

1. Решение 2-3 задач.

2. Решение 4-5 задач. Ответы на контрольные вопросы.

3. Решение 6-8 задач. Проверка правильности решения. Ответы на контрольные вопросы.

Контрольные вопросы:

1. Дать определение параллелепипеда.

2. Изобразить параллелепипед и все его элементы.

3. Перечислить виды параллелепипедов, их основные свойства.

Упражнения:

1. Два ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 1 и 5. Пло­щадь по­верх­но­сти этого па­рал­ле­ле­пи­пе­да равна 94. Най­ди­те тре­тье ребро, вы­хо­дя­щее из той же вер­ши­ны.

2. Два ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 10 и 10. Пло­щадь по­верх­но­сти па­рал­ле­ле­пи­пе­да равна 400. Най­ди­те его диа­го­наль.

3. Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около еди­нич­ной сферы. Най­ди­те его пло­щадь по­верх­но­сти.

4. Пло­щадь грани пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равна 20. Ребро, пер­пен­ди­ку­ляр­ное этой грани, равно 7. Най­ди­те объем па­рал­ле­ле­пи­пе­да.

5. Три ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 3, 3 и 24. Най­ди­те ребро рав­но­ве­ли­ко­го ему куба.

6. Одна из гра­ней пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да — квад­рат. Диа­го­наль па­рал­ле­ле­пи­пе­да равна 10 и об­ра­зу­ет с плос­ко­стью этой грани угол 30 . Най­ди­те объем па­рал­ле­ле­пи­пе­да.

7. Най­ди­те угол пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, для ко­то­ро­го , . Ответ дайте в гра­ду­сах.

8. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны длины рёбер: , . Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через вер­ши­ны , и .

Методические указания:

При решении использовать алгоритм решения задач:

1. Чертим прямоугольный параллелепипед.

2. Подписываем вершины. Отмечаем на чертеже упомянутые в условии точки. Соединяем линиями, где это необходимо.

3. Ставим известные (заданные) значения прямо на чертеже.

4. Если получился треугольник внутри тела, то выясняем есть ли в нем прямой угол и какой именно. Для этого пользуемся теоремами о перпендикуляре к плоскости или о трех перпендикулярах.

5. Чертим этот треугольник на плоскости. На нем также отмечаем заданные и искомые величины, если нужно, перенося числа с параллельных ребер.

6. Проводим необходимые вычисления по известным формулам. Как правило, это будут теорема Пифагора и определения синуса и косинуса острых углов прямоугольного треугольника.

Примеры выполнения упражнений:

Пример 1.

Два ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 3 и 4. Пло­щадь по­верх­но­сти этого па­рал­ле­ле­пи­пе­да равна 94. Най­ди­те тре­тье ребро, вы­хо­дя­щее из той же вер­ши­ны.

Решение:

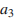Обо­зна­чим из­вест­ные ребра за и , а не­из­вест­ное за . Пло­щадь по­верх­но­сти па­рал­ле­ле­пи­пе­да вы­ра­жа­ет­ся как .

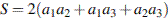Вы­ра­зим 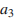: , от­ку­да не­из­вест­ное ребро

.

Ответ: 5.

Пример 2.

Одна из гра­ней пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да — квад­рат. Диа­го­наль па­рал­ле­ле­пи­пе­да равна 2 и об­ра­зу­ет с плос­ко­стью этой грани угол 30 . Най­ди­те объем па­рал­ле­ле­пи­пе­да.

Решение:

Длина диа­го­на­ли па­рал­ле­ле­пи­пе­да равна

.

Длина тре­тье­го ребра тогда 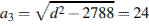. По­лу­чим, что объем па­рал­ле­ле­пи­пе­да

.

Ответ: 32256.

Пример 3.

Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около еди­нич­ной сферы. Най­ди­те его пло­щадь по­верх­но­сти.

Решение:

Вы­со­та и сто­ро­на та­ко­го па­рал­ле­ле­пи­пе­да равны диа­мет­ру сферы, то есть это куб со сто­ро­ной 2. Пло­щадь по­верх­но­сти куба со сто­ро­ной :

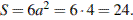
Ответ: 24.

Пример 4.

Диа­го­наль пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равна и об­ра­зу­ет углы 30 , 30 и 45 с плос­ко­стя­ми гра­ней па­рал­ле­ле­пи­пе­да. Най­ди­те объем па­рал­ле­ле­пи­пе­да.

Решение:

Ребро па­рал­ле­ле­пи­пе­да на­про­тив угла в равно , по­сколь­ку об­ра­зу­ет с за­дан­ной диа­го­на­лью и диа­го­на­лью одной из гра­ней рав­но­бед­рен­ный тре­уголь­ник. Два дру­гие ребра по по­стро­е­нию лежат в пря­мо­уголь­ных тре­уголь­ни­ках на­про­тив угла в и равны, по­это­му по­ло­ви­не диа­го­на­ли. Тогда объем па­рал­ле­ле­пи­пе­да:

Ответ: 4.

Рекомендуемая литература.

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М.: Просвещение, 2014. (Гриф Минобразования и науки РФ).

2. Башмаков М.И. Математика. Задачник: учеб. пособие для студ. учреждений сред. проф.

образования. — М.: Академия, 2014. (Гриф Минобразования и науки РФ).

3. Башмаков М.И. Математика: кн. для преподавателя: метод. пособие. — М.: Просвещение, 2013.

4. Богомолов Н.В. Математика. Учебник для СПО. – М.: Юрайт, 2015.

5. ЕГЭ по математике: подготовка к тестированию

http://www.uztest.ru

6. Математические этюды: 3D-графика, анимация и визуализация математических сюжетов

http://www.etudes.ru

Критерии оценки:

• ознакомление с условием задачи (анализ условия задачи и его наглядная интерпретация схемой или чертежом), 0,5 балла;

• составление плана решения задачи (составление уравнений, связывающих величины, которые характеризуют рассматриваемое явление с количественной стороны), 1 балл;

• подробное решение, 2 балла;

• проверка правильности решения (анализ полученного результата или числовой расчет), ответы на контрольные вопросы 1 балл;

• задача представлена на контроль в срок, 0,5 балла.

Максимальное количество баллов: 5

Оценка выставляется по количеству набранных баллов.

9. Тема 7.3.2 « Симметрия в кубе, в параллелепипеде, в призме и пирамиде. Решение задач»

Форма предоставления изученного материала (по программе самостоятельного изучения с указанием уровней сложности):

1. Решение 2-3 задач.

2. Решение 4-5 задач. Ответы на контрольные вопросы.

3. Решение 6-8 задач. Проверка правильности решения. Ответы на контрольные вопросы.

Контрольные вопросы:

1. Изобразите куб. Сколько центров симметрии имеет куб? Сколько осей симметрии имеет куб? Укажите некоторые оси симметрии на рисунке.

2. Продолжите предложение: точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры…

3. Изобразите параллелепипед. Сколько центров симметрии имеет параллелепипед? Сколько осей симметрии имеет параллелепипед? Укажите некоторые оси симметрии на рисунке.

4. Изобразите призму. Сколько центров и осей симметрии имеет призма, которую вы изобразили? Укажите некоторые оси симметрии на рисунке.

5. Изобразите пирамиду. Сколько центров и осей симметрии имеет пирамида, которую вы изобразили? Укажите некоторые оси симметрии на рисунке.

Упражнения:

1. Если каж­дое ребро куба уве­ли­чить на 4, то его пло­щадь по­верх­но­сти уве­ли­чит­ся на 240. Най­ди­те ребро куба.

2. В сосуд, име­ю­щ