РОЗРАХУНКОВО-ГРАФІЧНЕ ЗАВДАННЯ № 1

Тема 1

Побудова епюр внутрішніх силових факторів

У даній темі розглядається побудова епюр зусиль для балок та рам.

Балками називаються прямолінійні стержні, що працюють на згин. На розрахунковій схемі балка замінюється її віссю (рис. 1.1).

Рисунок 1.1.

Рамами називаються системи, що складаються з прямолінійних стержнів, які з’єднуються між собою жорстко або шарнірно. Вісь рами є ломаною лінією, але кожна прямолінійна ділянка її розглядається як балка. Вертикально розташовані стержні рами називають стояками, горизонтальні - ригелями (рис.1.2.).

Рисунок 1.2.

Усі навантаження, що діють на балку та раму, зведені до осі і силова площина співпадає з площиною рисунка. Балки та рами мають ті чи інші опорні закріплення – опори.

Конструктивні форми опор дуже різноманітні. Дія розрахунків опори схематизують у вигляді трьох основних типів:

1. Шарнірно - рухома опора: її реакція R_А, направлена вздовж опорного стержня (рис. 1.3.).

Рисунок 1.3.

2. Шарнірно-нерухома опора, в якій два опорні стержні приєднані спільним шарніром до осі балки (рис. 1.4.). Відповідно до кількості опорних стержнів (пов’язей) з боку опори на балку діють дві складові реакції, одна з яких діє вздовж осі балки (горизонтальна складова опорної реакції Н_А), а інша – перпендикулярно до осі балки (вертикальна реакція R_А). Поняття горизонтальна та вертикальна реакції умовні, оскільки вісь балки може мати довільний нахил.

Рисунок 1.4.

3. Затиснення (жорстке закріплення рис.1.5.), де виникають три складові опорної реакції: момент М_А, горизонтальна реакція Н_А та вертикальна R_А.

Опора моделюється трьома опорними стержнями, які перешкоджають як лінійним зміщенням точки обпирання, так і кутовому-повороту осі балки.

Рисунок 1.5.

Усі реакції та моменти вважаються прикладеними в точці А – центрі ваги опорного стержня.

Розглядаємо плоску систему сил, тому для визначення невідомих опорних реакцій можна скласти три рівняння статики (для систем статично визначених). SF_Х=О; SF_У=О; SМ=О.

Порядок обчислення опорних реакцій на практиці виконується в наступному порядку (рис. 1.6.):

Рисунок 1.6.

1. Позначаємо опори буквами А, В, (Рис 1.6.а).

2. Вибираємо напрямок реакцій та показуємо їх на силовій схемі (Рис 1.6.б).

3. Для схеми показаної на рисунку 1.6.а та 1.6.б три невідомі опорні реакції знаходимо з наступних рівнянь рівноваги:

а) сума проекцій усіх сил на горизонтальну вісь дорівнює нулю - SF_Х=0, звідси знаходиться Н_А;

б) сума моментів усіх сил відносно опорного шарніра А дорівнює нулю - SМ_А=0, звідси знаходиться Rв;

в) сума моментів відносно опорного шарніра В дорівнює нулю: SМв=0; звідси знаходиться R_А.

г) для перевірки правильності визначення опорних реакцій використовується така умова рівноваги, при якій сума проекцій усіх сил на вертикаль дорівнює нулю - SF_Y=0 або умова рівності нулю суми моментів усіх сил системи відносно точки (с) - SМс=0.

4. Для схеми (рис. 1.6.в, 1.6.г) послідовність визначення опорних реакцій наступна:

а) SF_Х=0, звідси знаходимо Н_A;

б) SF_У=0, знаходимо R_A;

в) SМ_A=0, звідси знаходимо М_A;

г) для перевірки використовуємо рівняння SМс=0.

Якщо навантаження перпендикулярне до осі бруса, то Н_A=0; якщо на балку діє розподілене навантаження, то для визначення реакцій його заміняють рівнодійною, яка прикладається в центрі ваги (ц.в.) цього навантаження і дорівнює його площі (рис.1.7)

Рисунок 1.7.

Якщо в результаті обчислень якась реакція буде від’ємною, тоді змінимо її напрямок на протилежний і в подальшому вважатимемо величину реакції додатною.

Послідовність визначення опорних реакцій залишається такою ж і для рам.

В усіх випадках, коли необхідно встановити та обчислити зусилля в балках та рамах застосовується метод перерізів. В довільному перерізі балки можуть виникати два зусилля: поперечна сила Q_y та згинальний момент М_z, а в рамах ще й поздовжня сила N_x.

Сили та моменти в різних перерізах балки різні. Графіки зміни внутрішніх силових факторів при переході від перерізу до перерізу вздовж балки називають епюрами.

При побудові дотримуються наступних правил:

1. Вісь на якій будують епюру, паралельна осі стержня.

2. Значення зусиль відкладають по нормалі до осі.

3. Епюри заштриховують відрізками перпендикулярними до осі.

4. Для сил та моментів обирають деякий масштаб. Ординати відкладають дотримуючись масштабу та проставляють на них числа, що вказують на величину характерних ординат, а в полі епюр зазначають знак зусилля.

5. Епюра згинального моменту будується з боку розтягнутих волокон, тобто додатні значення відкладають вниз, а від’ємні значення – вгору.

Перш ніж будувати епюри, стержень розбивають на ділянки. Для балки, навантаженої зосередженими силами, ділянкою є частина стержня між точками прикладання зосереджених сил. Якщо на стержень діє розподілене навантаження, ділянкою називають частину стержня, в межах якої розподілене навантаження змінюється за одним законом.

На основі закону рівноваги складаємо вирази для М_z, Q_y, N_x в довільному перерізі кожної ділянки. Графіки цих залежностей і є епюрами.

Правило знаків для зусиль (рис. 1.8):

а) для згинальних моментів (М_z)

б) для поперечних сил (Q_y);

в) для поздовжніх сил (N_x)

Рисунок 1.8

Розглянемо приклади побудови епюр зусиль балок і рам.

Приклад 1. Для заданої балки (рис. 1.9) побудувати епюри М_z та Q_y.

Вхідні дані: g= 4 кн/м; F= 5 кн; М= 1 кн м.

Рисунок 1.9.

1. Позначаємо опори А, В.

2. Складаємо силову схему вказуючи попередній напрямок реактивних сил.

3. Визначаємо опорні реакції.

SF_Х=О; Н_A=О

SМв=О; = 0

R_A =19.6 кн

SМа=0; = 0

Rв=17.4 кн

Перевірка: SF_Y=0; 19.6 + 17.4 – = 0

4. Вибираємо перерізи х.

5. Для кожного перерізу записуємо рівняння для поперечної сили Q_y та згинального моменту М_z. Будуємо епюри з використанням правила знаків приведеного на рис.1.8.

Переріз Х1. м

Qy = 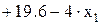x₁ = 0 Q_y = + 19.6 Кн

x₁ = 8 Q_y = Кн

Епюра Q_y перетинає вісь, в точці перетину згинальний момент матиме екстремальне значення, що витікає з диференціальної залежності _.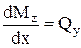

Для визначення значення відстані х₁ при якому згинальний момент досягає свого максимального значення, прирівняємо до нуля вираз для поперечної сили Q_y.

м.

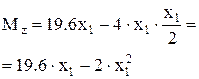
До виразу для М_z змінна х входить у другому ступені, тобто М_z – квадратична парабола, а вираз для Q_y– в першому ступені, а це означає, що Q_y – пряма лінія.

На підставі сказаного будуємо епюри Q_y та М_z (рис.1.9).

Переріз Х2. м

Кн

Переріз Х3. м

Q_y =0 M_z= -1 Кн м

Переріз Х4. м

Q_y= Кн

Приклад 2. Для заданої балки (рис.1.10.) побудувати епюри внутрішніх зусиль.

1. Визначимо опорні реакції.

Оскільки М_А має знак мінус змінюємо його напрямок на протилежний, тобто за годинниковою стрілкою.

Перевірка: SМс=0;

2. Проведемо перерізи і для кожного з них запишемо рівняння Q_y, та М_z і побудуємо епюри.

Рисунок 1.10.

Переріз Х1. м

Q_y = -7 Кн

M_z =

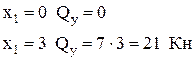
Переріз Х2. м

Q_y = Кн.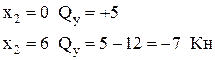

Приклад 3. Побудувати епюри Q_y, M_z, N_x для заданої рами (Рис.1.11)

1. Визначаємо опорні реакції

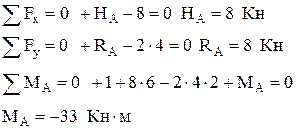
Перевірка:åМс = 0;

2. Будуємо епюру зусиль.

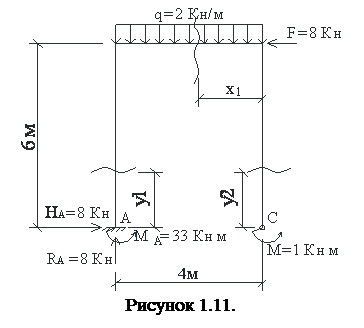Для визначення зусиль в рамі розглянемо переріз на кожному її елементі. Вертикальні елементи рами (стояки) розглядаємо справа. Епюри М_z, Q_y, N_x в рамі будуються на контурі рами.

Переріз Y1.

Q_y = -8 Кн

N_x = -8 Кн

Переріз Y2.

Q_y = 0

M_z = -1 Кн м

N_x = 0

Переріз X1.

x₁ = 0 Q_y = 0

x₁ = 4 Q_y = +8 Кн

N_x = -8 Кн

Епюра Q_y Епюра М_z Епюра N_x

Рисунок 1.12.

РОЗРАХУНКОВО-ГРАФІЧНЕ ЗАВДАННЯ № 1

Date: 2016-05-25; view: 954; Нарушение авторских прав