Функционально полные наборы и базисные наборы

Функционально полным называется набор булевых функций { f₁, f₂,…, f_n} такой, что любая сколь угодно сложная булева функция может быть выражена в виде суперпозиции (сочетания) функций из этого на­бора.

Базисным называется такой функционально полный набор, из кото­рого нельзя исключить ни одну булеву функцию без ущерба для его функциональной полноты.

Поскольку любая булева функция, заданная таблицей истинности, может быть представлена в виде СДНФ (или СКНФ), то набор

1) {&, Ú,) - функционально полный набор.

Набор 1) не является базисным набором, так как из него можно исклю­чить либо &, либо Ú, а недостающую функцию реализовать с помощью оставшихся функций. Например, если из набора 1) исключена &, то ее можно реализовать так: АВ = (A Ú B) (выражение справа понимает­ся так: 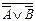). Если же из набора 1) исключена функция v, то она может быть реализована так: XÚY= (XY)= .

Таким образом, получаем два функционально полных (базисных) на­бора:

2) {&, };

3) {Ú, }.

Русский математик Жегалкин показал, что любая булева функция может быть представлена с использованием операций конъюнкции (&) сложения по модулю 2 (Å) и константы 1. Покажем, как извест­ные функции набора 1) представить в виде декомпозиции функций Жегалкина: А = А Å 1; A Ú В = (А В) = (А Å1)(В Å 1) Å 1 = АВ Å А Å В Å 1 Å 1=АВ Å А Å В.

Поэтому следующим функционально полным (базисным) набором будет набор функций Жегалкина:

4) {&, Å, 1 }.

Аналогично можно показать, что набор

5) {v, Å, 1} - базисный набор.

Выше было показано, что мажоритарная функция М(Х, Y, Z) = XY v XZ v YZ. Если на один из входов, например Z, подать константу 1, то получим М(Х, Y, 1) = XY v X v Y=X v Y, а если на этот же вход Z подать константу 0, то получим М(Х, Y, 0) = XY. Поэтому получаем еще два базисных набора:

6) {М,, 1};

7) {М,, 0};

Когда говорят о "мажоритарном базисе", то имеют в виду эти два набора (или их объединение: {М,, 1,0}), предполагая, что 1 и 0 реали­зуются "без затрат", а инверсия аргументов всегда присутствует, если комбинационная схема подключается к триггерным устройствам (эле­ментарным автоматам), которые имеют как прямой, так и инверсные выходы.

На практике, как правило, используются базисные наборы, состоя­щие только из одной функции ("штрих Шеффера" или "стрелка Пирса"):

8) {/};

9) { ¯ }.

Набор 8) реализует функцию (XY) = 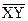. Инверсия аргумента мо­жет быть получена так: X = (XX). Конъюнкция XY = ((XY) = 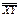= . Дизъюнкция может быть реализована так: X v Y = (ХУ)= = .

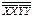Набор 9) реализует функцию (X v У) = 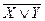. Инверсия аргумента может быть получена так: (X v X). Дизъюнкция может быть полу­чена так: X v Y= ((X v Y)). Конъюнкция может быть получена так: XY=(X v Y).

Пример. Перевести в базис Шеффера и Пирса функцию, задан­ную в дизъюнктивной форме:

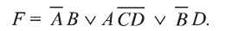
В базисе Шеффера функция будет иметь вид

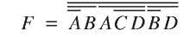
В базисе Пирса функция будет иметь вид

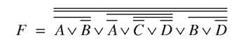
Date: 2016-05-25; view: 2321; Нарушение авторских прав