Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






График решения задач для аудиторной и домашней работы

Стр 1 из 20Следующая ⇒




РАБОЧАЯ ТЕТРАДЬ

ПО ДИСЦИПЛИНЕ

«СТАТИСТИКА»

 

 

Оглавление

I. ЗАДАНИЯ ДЛЯ АУДИТОРНОЙ РАБОТЫ………………………  
  График решения задач для аудиторной и домашней работы……….  
  Тема 1. «Выборочный метод»…………………………………………  
  Тема 2. «Проверка статистических гипотез»………………………...  
  Тема 3. «Корреляционно – регрессионный анализ»………………...  
  Тема 4. «Ряды динамики»……………………………………………...  
  Тема 5. «Экономические индексы»……………………………….......  
II. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ…………….  
III. ТИПОВОЙ РАСЧЕТ…………………………………………………  
IV. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ……………………………………  
  Тема 1. «Выборочный метод»…………………………………………  
  Тема 2. «Проверка статистических гипотез»………………………...  
  Тема 3. «Корреляционно – регрессионный анализ»………………...  
  Тема 4. «Ряды динамики»……………………………………………...  
  Тема 5. «Экономические индексы»……………………………….......  
V. ПРИЛОЖЕНИЯ……………………………………………………….  
  1. Экзаменационные вопросы по курсу «Статистика»………………  
  2. Критерии оценки работы студента при изучении дисциплины «Статистика»……………………………………………………………  
  3. Таблицы………………………………………………………………  
  4. Литература…………………………………………………………...  
     
     

I. ЗАДАНИЯ ДЛЯ АУДИТОРНОЙ РАБОТЫ

В первой части рабочей тетради собраны задания для аудиторной работы, выполняемой студентами всех факультетов.

Задания выполняются в соответствии с графиком решения задач. Если задачи, запланированные к решению на данном занятии студентом не выполнены, то он выполняет их во внеаудиторное время. Каждое выполненное задание оценивается преподавателем и им выставляется оценка, формирующая итоговый балл студента по дисциплине.

Задания выполняются в тетради в клетку пастой любого цвета кроме красного. Начало задания нумеруется. Где это требуется, в конце задания записывается ответ, проводится анализ расчетов, делаются соответствующие выводы. Таблицы записываются от руки. Графики и чертежи рисуются от руки на миллиметровой бумаге.


График решения задач для аудиторной и домашней работы

Тема Номер занятия Тема занятия Число часов на занятие Номер задачи
ДМО ДФО ДМРО ДАО ДБО ДМБ ДИО ДИС ДМС ДФС ДБС
1. 1. Группированный статистический ряд.       0,5     1.1, 1.2, 1,3
2. Графическое представление выборки.       0,5     1.4 1), 1.5 1), 1,6 1)
3. Квантиль.       0,5     1.4 2), 1.5 2), 1,6 2)
4. Квартиль, дециль, перцентиль.             1.10, 1.11, 1.12
5. Средние значения и показатели вариации.       0,5     1.16, 1.17, 1.18
6. Метод моментов.       0,5     1.22, 1.23, 1.24
7. Доверительная вероятность. Доверительный интервал. Интервальная оценка величины математического ожидания. Интервальная оценка величины генеральной средней.       0,5     1.28, 1.29, 1.30, 1.34, 1.35, 1.36, 1.37, 1.38
8. Итоговое занятие по теме.       0,5     1.7, 1.8, 1.9 1.13, 1.14, 1.15 1.19, 1.20, 1.21 1.25, 1.26, 1.27 1.31, 1.32, 1.33
2. 9. Проверка гипотезы о нормальном распределении генеральной совокупности.       0,5     2.1, 2.2, 2.3
10. Итоговое занятие по теме.       0,5     2.4, 2.5, 2.6
3. 11. Эмпирические линии регрессии.       0,5     3.1 1), 2), 3.2 1), 2), 3.3 1), 2), 3.4 1), 2), 3.5 1), 2), 3.6 1), 2)
12. Коэффициент линейной корреляции и его свойства.       0,5     3.1 3), 3.2 3), 3.3 3), 3.4 3), 3.5 3), 3.6 3)
13. Корреляционное отношение и его свойства.       0,5     3.1 4), 3.2 4), 3.3 4), 3.4 4), 3.5 4), 3.6 4)
14. Статистическая значимость эмпирических данных.       0,5     3.1 5), 3.2 5), 3.3 5), 3.4 5), 3.5 5), 3.6 5)
15. Расчет параметров линейной, параболической и показательной линий регрессии.       0,5     3.1 6), 3.2 6), 3.3 6), 3.4 6), 3.5 6), 3.6 6)
16. Точность регрессионной модели. Выбор наиболее точной модели.       0,5     3.1 7), 8), 9), 3.2 7), 8), 9), 3.3 7), 8), 9), 3.4 7), 8), 9), 3.5 7), 8), 9), 3.6 7), 8), 9)
  Прогноз значений признаков.       0,5     3.1 10), 11), 3.2 10), 11), 3.3 10), 11), 3.4 10), 11), 3.5 10), 11), 3.6 10), 11)
18. Итоговое занятие.       0,5     3.7, 3.8
19. Отбор значимых признаков (переход к двухфакторной модели).       0,5     3.9 1), 3.10 1), 3.11 1)
20. Множественный коэффициент корреляции. Определение степени линейности и тесноты корреляционной связи.       0,5     3.9 2), 3.10 2), 3.11 2)
21. Расчет параметров линейной модели.       0,5     3.9 3), 3.10 3), 3.11 3)
22. Статистическая значимость эмпирических данных. Точность регрессионной модели.       0,5     3.9 4), 5), 6), 3.10 4), 5), 6), 3.11 4), 5), 6)
22. Исключение из модели наименее значимого факторного признака. Переход к двухфакторной модели.       0,5     3.9 7), 8), 9), 3.10 7), 8), 9), 3.11 7), 8), 9)
23. Итоговое занятие.       0,5     3.12
4. 24. Сравнение уровней ряда динамики цепным и базисным способами.       0,5     4.1 1), 4.2 1), 4.3 1), 4.4 1), 4.5 1), 4.6 1), 4.7 1), 4.8 1)
25. Среднее значение уровней ряда динамики и его числовых характеристик.       0,5     4.1 2), 4.2 2), 4.3 2), 4.4 2), 4.5 2), 4.6 2), 4.7 2), 4.8 2)
  26.   Функция тренда.         0,5         4.12 1), 4.13 1), 4.14 1), 4.15 1), 4.16 1), 4.17 1), 4.18 1), 4.19 1)
27. Индексы сезонности.       0,5     4.10, 4.11
  28.   Уравнение Фурье.         0,5         4.12 2), 4.13 2), 4.14 2), 4.15 2), 4.16 2), 4.17 2), 4.18 2), 4.19 2)
29. Прогнозирование уровней ряда динамики.       0,5     4.12 3), 4), 5), 4.13 3), 4), 5), 4.14 3), 4), 5), 4.15 3), 4), 5), 4.16 3), 4), 5), 4.17 3), 4), 5), 4.18 3), 4), 5), 4.19 3), 4), 5)
30. Итоговое занятие по теме.       0,5     4.9, 4.20, 4.21, 4.22, 4.23, 4.24, 4.25
5. 31. Индивидуальные индексы.       0,5     5.1 1), 5.2 1), 5.3 1)
32. Агрегатные индексы. Индексы переменного, постоянного состава, структурных сдвигов.       0,5     5.1 2), 3), 4), 5.2 2), 3), 4), 5.3 2), 3), 4), 5.5, 5.6, 5.7, 5.9, 5.10, 5.11, 5.12, 5.13
33. Территориальные индексы.       0,5     5.15, 5.16, 5.17, 5.18, 5.19
34. Итоговое занятие по теме.       0,5     5.4, 5.8, 5.14, 5.20

Тема 1. «Выборочный метод»

 

В упражнениях 1.1 – 1.3 необходимо составить группированный статистический ряд.

1.1. Дан пробег каждого из 55 фургонов транспортной компании в течение дня (км.):

 

                     
                     
                     
                     
                     
                     

1.2. Дано время решения контрольной задачи пятьюдесятью учениками в секундах:

 

                   
                   
                   
                   
                   

 

1.3. Дана продолжительность работы шестидесяти пяти электронных ламп (в часах) одного типа:

 

13,4 14,7 15,2 15,1 13,0 8,8 14,0 17,9 15,1 16,5 16,6
14,2 16,3 14,6 11,7 16,4 15,1 17,6 14,1 18,8 11,6 13,9
18,0 12,4 17,2 14,5 16,3 13,7 15,5 16,2 8,4 14,7 15,4
10,1 10,7 16,9 15,8 16,1 12,3 14,0 17,7 14,7 16,2 17,1
17,7 15,8 18,3 17,5 12,7 20,7 13,5 14,0 15,7 21,9 14,3
11,3 15,4 10,9 18,2 17,3 15,2 16,7 17,3 12,1 19,2  

 

В упражнениях 1.4 – 1.6 по выборкам из упражнений 1.1 – 1.3 необходимо: 1) построить полигон частот, гистограмму и кумулятивную кривую; 2) определить квантиль порядка p = 0,15, 0,35 и 0,6; 3) найти вероятность нахождения значения случайной величины в интервале .

 

1.4. Упражнение 1.1, .

1.5. Упражнение 1.2,

1.6. Упражнение 1.3,

 

1.7. По полигону частот (рисунок 1) построить группированный статистический ряд.

1.8. По гистограмме частот (рисунок 2) построить группированный статистический ряд.

1.9. По кумулятивной кривой (рисунок 3) построить группированный статистический ряд (объем выборки принять равным 100).

 

Рис.1

 

 
0,5
 
 
 
 
 
 
x
 

 

 

Рис. 2

 

 

 
 

 

 


Рис.

 
3

 

В упражнениях 1.10 – 1.15 по выборкам из упражнений 1.1 – 1.3 и 1.7 – 1.9 необходимо найти верхние и нижние квартили, децили и перцентели, моду и медиану, сделать соответствующие выводы.

 

1.10. Упражнение 1.1.

1.11. Упражнение 1.2.

1.12. Упражнение 1.3.

1.13. Упражнение 1.7.

1.14. Упражнение 1.8.

1.15. Упражнение 1.9.

 

В упражнениях 1.16 – 1.21 по выборкам из упражнений 1.1 – 1.3 и 1.7 – 1.9 необходимо найти среднее арифметическое, среднее линейное отклонение, дисперсию (двумя способами: по определению и по формуле разностей), среднее квадратическое отклонение, коэффициент вариации, коэффициент осцилляции, ассиметрию и эксцесс, сделать соответствующие выводы.

 

1.16. Упражнение 1.1.

1.17. Упражнение 1.2.

1.18. Упражнение 1.3.

1.19. Упражнение 1.7.

1.20. Упражнение 1.8.

1.21. Упражнение 1.9.

 

В упражнениях 1.22 – 1.27 по выборкам из упражнений 1.1 – 1.3 и 1.7 – 1.9 необходимо методом моментов найти среднее арифметическое, дисперсию, ассиметрию и эксцесс, сделать соответствующие выводы.

 

1.22. Упражнение 1.1.

1.23. Упражнение 1.2.

1.24. Упражнение 1.3.

1.25. Упражнение 1.7.

1.26. Упражнение 1.8.

1.27. Упражнение 1.9.

 

В упражнениях 1.28 – 1.33 по выборкам из упражнений 1.1 – 1.3 и 1.7 – 1.9 необходимо: 1) с вероятностью γ определить границы интервала, в котором заключено математическое ожидание a; задачу решить в предположении а) повторного, б) бесповторного отбора из генеральной совокупности объема N; 2) определить границы интервала, в котором заключена генеральная доля признака, выборочную долю рассчитать для интервала ; 3) сделать соответствующие выводы.

 

1.28. Упражнение 1.1, γ = 0,997, N=1500, = .

1.29. Упражнение 1.2. γ = 0,683, N=800, = .

1.30. Упражнение 1.3. γ = 0,954, N=1000, = .

1.31. Упражнение 1.7. γ = 0,683, N=900, = .

1.32. Упражнение 1.8. γ = 0,954, N=840, = .

1.33. Упражнение 1.9. γ = 0,997, N=950, = .

 

1.34. Средняя ошибка выборки равна 0,5, а предельная – 1,45. Чему равна доверительная вероятность?

1.35. Что произойдет с предельной ошибкой выборки, если ее объем а) увеличить в два раза, б) уменьшит в полтора раза?

1.36. Что произойдет с предельной ошибкой выборки, если доверительная вероятность а) увеличится с 0,683 до 0,997, б) уменьшится с 0,997 до 0,954?

1.37. Дисперсия уменьшилась на 20%. Как это изменение повлияет на объем выборки?

1.38. Среднее значение выборочной совокупности равно 0,4, средний квадрат – 0,25, объем выборки n = 80, а объем генеральной совокупности N = 3200. С вероятностью 0,954 определить границы интервала, в котором заключено значение математического ожидания.

 

Тема 2. «Проверка статистических гипотез»

В упражнениях 2.1 – 2.6 по данным упражнений 1.1 – 1.3 и 1.7 – 1.9 необходимо с доверительной вероятностью 0,95 проверить гипотезу о том, что генеральная совокупность, которой принадлежит выборка, распределена по нормальному закону.

 

2.1. Упражнение 1.1.

2.2. Упражнение 1.2.

2.3. Упражнение 1.3.

2.4. Упражнение 1.7.

2.5. Упражнение 1.8.

2.6. Упражнение 1.9.

Тема 3. «Корреляционно – регрессионный анализ»

В упражнениях 3.1 – 3.6 необходимо: 1) произвести все необходимые вычисления (рассчитать среднее значение и показатели вариации по определению и методом моментов); 2) построить эмпирические линии регрессии и сделать первоначальные выводы о форме корреляционной связи; 3) определить величину коэффициента линейной корреляции (по определению и методом моментов) и сделать выводы о форме корреляционной зависимости; 4) найти значение корреляционного отношения и сделать выводы о тесноте корреляционной связи; 5) с вероятностью 0,95 проверить гипотезу о статистической значимости эмпирических данных; 6) установить вид уравнения регрессии в предположении прямой (расчет коэффициентов произвести двумя способами), параболической и показательной регрессионной моделей; 7) с помощью величины средней ошибки аппроксимации отобрать наиболее точную модель; 8) найти индекс детерминации для каждой из построенных моделей и сделать соответствующие выводы; 9) используя результаты пунктов 7 и 8 отобрать наилучшую модель; 10) построить на одном чертеже эмпирические данные и линии регрессии; 11) произвести прогноз значения y при 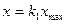и x при , где значения и соответствуют последнему номеру упражнения, деленному на 5 и 10 соответственно.

 

3.1. Распределение прямоугольных плиток по длине x (см) и весу y (кг):

x y          
             
             
             
             
             
           


3.2. Распределение заводов по основным фондам x и по готовой продукции y (млн. руб.):

x y          
             
             
             
             
             
           

 

3.3. Распределение растений по весу каждого из них x и по весу семян y (г.):

x y          
             
             
             
             
             
           

 

3.4. Распределение предприятий по объему продукции x и по ее себестоимости y (тыс. руб.):

x y          
2,0            
2,5            
3,0            
3,5            
4,0            
           

 

3.5. Распределение проб руды по содержанию окиси железа x и закиси железа y (%):

x y              
                 
                 
                 
                 
                 
                 
               

 

 

3.6. Распределение однотипных предприятий по основным фондам x (млн. руб.) и себестоимости единицы продукции y (руб.):

x y          
1,25            
1,50            
1,75            
2,00            
2,25            
           

 

В упражнениях 3.7 – 3.8 необходимо заполнить корреляционную таблицу и выполнить упражнения, аналогичные 3.1 – 3.6.

3.7.

x y (10;12) (12;14) (14;16) (16;18) (18;20)
(0;3) ?         ?
(3;6)           ?
(6;9)       ?    
(9;12)   ?        
(12;15)           ?
  ? ? ? ? ?

 

3.8.

x y (2;6) (6;10) (10;14) (14;18) (18;22)
(4,5;14,5)         ?  
(14,5;24,5)         ?  
(24,5;34,5)       ?    
(34,5;44,5)     ?     ?
(44,5;54,5) ?          
? ?   ? ? ?

 

 

В упражнениях 3.9- 3.12 необходимо: 1) найти парные коэффициенты корреляции и с помощью t – критерия Стьюдента (вероятность принять равной 0,95) исключить один из факторных признаков, перейти к двухфакторной регрессии; 2) вычислить множественный коэффициент корреляции и сделать выводы о форме и силе корреляционной зависимости; 3) с помощью F – критерия Фишера с вероятностью 0,95 оценить статистическую значимость эмпирических данных; 4) вычислить значение общего индекса детерминации; 5) двумя способами получить уравнение линейной модели множественной регрессии; 6) по величине средней ошибки аппроксимации оценить точность линейной модели; 7) подсчитать дельта – коэффициенты; 8) найти значения коэффициентов эластичности; 9) исключить из модели один из факторных признаков и перейти к модели с парной регрессией.

3.9.

507,2 19,5 352,9 448,1
506,6 19,8 187,1 459,9
487,8 21,1 375,2 447,9
496,0 18,6 287,9 444,3
493,6 19,6 444,0 411,7

 

3.10.

328,6 429,3 459,5 10,5
314,7 386,9 511,3 13,6
259,4 311,5 328,6 10,8
187,7 302,2 350,0 10,9
411,7 458,9 462,4 11,7

3.11.

10,3 262,0 238,5 298,7
10,6 242,4 269,4 529,3
8,5 231,9 284,0 320,0
6,7 214,3 172,3 502,0
8,3 208,4 166,4 194,9

3.12.

3,5   4,8 71,34
6,7   5,1 73,41
3,2   5,2 73,03
3,9   7,0 74,84
3,5   5,3 75,13
5,0   7,5 76,17
3,7   7,7 63,42
5,0   7,3 80,13
3,8   7,0 82,46
5,0   6,7 84,42

 

 

Тема 4. «Ряды динамики»

 

В задачах 4.1 – 4.8 необходимо: 1) определить тип ряда динамики; 2) произвести анализ уровней ряда динамики цепным и базисным способами (за базисный принять первый уровень); 3) рассчитать средние характеристики уровней ряда динамики.

 

4.1. Даны объемы выпуска продукции А в 2007 году (тыс. шт.):

Месяцы Январь Февраль Март Апрель Май Июнь
Выпуск продукции А тыс. шт. 16,6 15,6 16,2 14,6 18,0 18,2
Месяцы Июль Август Сентябрь Октябрь Ноябрь Декабрь
Выпуск продукции А тыс. шт. 19,1 19,3 14,6 16,0 17,0 18,1

4.2. Число работающих на предприятии в 2000 – 2006 характеризовались следующими данными (на конец года), тыс.чел.:

Годы              
Количество работающих, чел.              

4.3. Сведения о величине товарооборота торгующей организации в 2006 году (тыс. у. е.):

Месяцы Январь Апрель Май Июнь Август Октябрь Декабрь
Товарооборот, Тыс. у. е. 17,2 18,2 14,6 13,4 14,0 20,0 22,5

4.4. Уровень компьютеризации фирмы (количество персональных компьютеров на сто работающих) в 1994 – 2004годах характеризовался следующими данными (на конец года):

Годы              
Уровень компьютеризации, комп./100чел. 0,52 0,70 1,02 2,25 4,28 5,50 10,50

4.5. Площадь складских помещений предприятия в 1999 – 2004 годах, тыс. кв. м.:

Годы            
Площадь складских помещений, тыс. кв. м. 10,5 17,4 17,7 20,8 23,4 25,6

 

 

4.6. Премиальный фонд фирмы (тыс. руб.) в 2007 году характеризовался следующими данными (на начало месяца):

Месяцы Январь Февраль Март Апрель Май Июнь
Премиальный фонд, тыс. руб.            
Месяцы Июль Август Сентябрь Октябрь Ноябрь Декабрь
Премиальный фонд, тыс. руб.            
Месяцы Январь 2008 г.          
Премиальный фонд, тыс. руб.            

4.7. Количество уволенных с предприятия (чел.) в 1992 – 2004 годах:

Годы              
Количество уволенных, чел.              

4.8. Количество рекламаций на производство товара (шт.) на конец месяца в 2004 году:

Месяцы Декабрь 2003 Январь Апрель Март
Количество рекламаций, шт.        
Месяцы Август Сентябрь Ноябрь Декабрь
Количество рекламаций, шт.        

4.9. В упражнении 4.1 найти индексы сезонности, сделать чертеж, проанализировать полученные результаты.

 

В упражнениях 4.10 – 4.11 по выпуску продукции в 2002 – 2007 годах (тыс. шт.) необходимо: 1) найти индексы сезонности по каждому году и в целом за три года; 2) полученные результаты представить графически на одном чертеже; 3) проанализировать полученные результаты.

Таблица 1.

Месяцы Годы
           
Январь 11,35 15,00 14,40 18,50 20,00 24,10
Февраль 11,00 14,95 14,45 18,00 21,15 24,05
Март 9,50 14,00 13,74 17,75 21,00 23,95
Апрель 9,45 13,80 13,50 17,32 19,71 24,01
Май 9,40 13,75 13,24 17,50 19,66 25,15
Июнь 10,00 13,70 14,00 17,62 20,04 26,09
Июль 12,00 14,15 15,00 17,62 21,35 25,78
Август 12,15 14,18 15,40 17,44 22,44 25,55
Сентябрь 10,95 15,00 16,00 17,30 23,15 26,10
Октябрь 12,20 14,00 17,44 17,25 23,41 26,32
Ноябрь 14,45 13,95 17,50 17,15 23,93 26,41
Декабрь 15,25 13,00 18,00 19,20 24,27 26,50

4.10. 2002 – 2004 годы.

4.11. 2005 – 2007 годы.

 

В упражнениях 4.12 – 4.23 необходимо: 1) найти вид линейной функции тренда; 2) построить модель ряда динамики в виде уравнения Фурье (число гармоник принять равным 1, 2 и 3); 3) осуществить по построенным моделям прогноз на следующий период; 4) на одном графике изобразить эмпирические данные и построить графики найденных функций; 5) проанализировав график отобрать модель, с помощью которой возможен наиболее точный прогноз.

 

4.12. Упражнение 4.1.

4.13. Упражнение 4.2.

4.14. Упражнение 4.3.

4.15. Упражнение 4.4.

4.16. Упражнение 4.5.

4.17. Упражнение 4.6.

4.18. Упражнение 4.7.

4.19. Упражнение 4.8.

4.20. Таблица 1. Данные 2002 года.

4.21. Таблица 1. Данные 2003 года.

4.22. Таблица 1. Данные 2004 года.

4.23. Таблица 1. Данные 2005 года.

4.24. Таблица 1. Данные 2006 года.

4.25. Таблица 1. Данные 2007 года.

 

 

Тема 5. «Экономические индексы»

Деятельность предприятия по производству товаров A – I в 2006 – 2007 годах характеризуется следующими данными:

Таблица 2.

Товар Себестоимость, руб./ шт. Цена изделия, руб./шт. Объем выпуска, тыс. шт. Время на производство, ед. прод./ч.
               
A 0,45 0,48 1,02 1,15 15,0 17,0 0,70 0,60
B 2,35 2,14 3,10 3,15 23,5 44,7 0,45 0,22
C 7,50 7,90 10,00 10,34 19,3 14,6 0,33 0,32
D 0,95 1,02 1,50 1,47 42,0 43,0 0,41 0,44
E 2,15 2,40 3,50 3,64 14,4 13,2 0,71 0,70
F 4,15 4,07 5,00 5,44 11,6 12,4 1,02 1,01
G 256,00 280,35 264,50 295,72 4,4 4,6 0,35 0,38
H 77,31 77,15 80,42 81,43 6,8 7,3 0,47 0,52
I 15,30 16,01 17,72 17,71 13,2 11,0 2,30 2,25

 

В упражнениях 5.1 – 5.4 по данным таблицы 2 необходимо: 1) вычислить индивидуальные и сводные индексы себестоимости, цен, объема, затрат и товарооборота; 2) определить сводные индексы цен и объема, используя средние взвешенные формулы, результаты сравнить с вычислениями п. 1); 3) определить величину экономии предприятия от изменения себестоимости и величину экономии покупателя от изменения цен; 4) дать анализ полученных результатов.

 

5.1. Предприятия A, B,C.

5.2. Предприятия C, D, E.

5.3. Предприятия E, F, G.

5.4. Предприятия G, H, I.

 

В упражнениях 5.5 – 5.8 по данным таблицы 2 необходимо: 1) вычислить индивидуальный индекс производительности труда; 2) определить сводный индекс производительности труда, взвешенный по трудоемкости; 3) найти сводный индекс производительности труда, взвешенный по выработке; 4)подсчитать средний индекс производительности труда, взвешенный по трудоемкости.

 

5.5. Предприятия A, B,C.

5.6. Предприятия C, D, E.

5.7. Предприятия E, F, G.

5.8. Предприятия G, H, I.

 

В упражнениях 5.9 – 5.14 по данным о реализации товара А в четырех регионах 2006 – 2007 годах определить индексы цен переменного и фиксированного состава, а также индекс структурных сдвигов. Дать анализ полученных результатов.

Регион 2006 г. 2007 г.
Цена, руб./шт. Продано, тыс. шт. Цена, руб./шт. Продано, тыс. шт.
  17,42 42,3 18,05 40,2
  16,15 35,7 17,01 36,2
  14,48 38,7 14,32 41,5
  13,92 39,9 13,60 40,7

 

5.9. Регионы 1 и 2.

5.10. Регионы 1 и 3.

5.11. Регионы 1 и 4.

5.12. Регионы 2 и 3.

5.13. Регионы 2 и 4.

5.14. Регионы 3 и 4.

 

В упражнениях 5.15 – 5.20 по ценам и объемам реализации товаров 1 – 5 в двух регионах А и Б найти территориальный индекс цен двумя способами и индекс физического объема реализации.

Товар Регион А Регион Б
Цена, у. е./шт. Продано, тыс. шт. Цена, у. е./шт. Продано, тыс. шт.
  0,53   0,54  
  1,77   1,75  
  1,41   1,35  
  0,95   0,89  
  2,36   2,42  

 

5.15. Товары 1, 2, 3.

5.16. Товары 1, 2, 4.

5.17. Товары 1, 2, 5.

5.18. Товары 2, 3, 4.

5.19. Товары 2, 3, 5.

5.20. Товары 3, 4, 5.

 

12345678910Следующая ⇒

Date: 2016-05-25; view: 1652; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.007 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию