Основні теоретичні відомості. Відповідно до теореми Котельникова будь який неперервний сигнал з верхньою частотою спектра може бути повністю відновлений

Теорема, яку доведено В. А. Котельниковим, є одним з фундаментальних положень теоретичної радіотехніки. Теорема встановлює можливість як завгодно точного відновлення миттєвих значень сигналу з обмеженим спектром, виходячи з відлікових значень (вибірок), взятих через рівні проміжки часу.

Відповідно до теореми Котельникова будь який неперервний сигнал 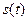з верхньою частотою спектра може бути повністю відновлений, якщо відомі відлікові значення цього сигналу, узяті через рівні проміжки часу за формулою:

, (7.1)

де 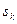– відліки сигналу, узяті через рівні проміжки часу , (рис. 7.1).

Рис. 7.1. Сигнал та його відліки

На практиці ця теорема має величезне значення. Наприклад, відомо, що більшість звукових сигналів можна з деякою мірою точності вважати сигналами з обмеженим спектром. Їх спектр, в основному, лежить нижче 20 кГц. Це означає, що при дискретизації з частотою не менш 40 кГц, ми можемо достатньо точно відновити вихідний аналоговий звуковий сигнал по його цифровим відлікам. Абсолютної точності досягти не вдасться, оскільки в природі не буває сигналів з ідеально обмеженим спектром. При цьому ряд Котельникова використовують для наближеного опису такого сигналу.

Під час використання теореми Котельникова необхідно враховувати наступні фактори:

1. Сигнали з обмеженим спектром мають бути нескінченні у часі, тому відновлення миттєвих значень 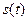вимагає врахування нескінченного числа дискретних відліків. Якщо використовувати відліки, які знаходяться в обмеженому інтервалі спостереження, то це призводить до виникнення помилок відновлення.

2. Сигнали скінченної тривалості теоретично мають нескінченні частотні спектри. У загальному випадку 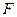обирають таким чином, щоб в діапазоні частот від 0 до 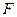знаходилася основна частина енергії сигналу. При цьому похибки відновлення будуть збільшуватися зі збільшенням частини енергії, що знаходиться за межами обраної смуги частот від 0 до .

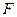3. Появу додаткових похибок відновлення за дискретними відліками Котельникова викликають відхилення характеристик реальних фільтрів нижніх частот від ідеальних.

Нехай є прямокутний відеоімпульс із одиничною амплітудою й тривалістю , що не належить до числа сигналів з обмеженим спектром, але модуль його спектральної щільності досить швидко (пропорційно 1/ 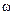) зменшується з ростом частоти.

Якщо описати цей сигнал двома відліками на початку й наприкінці імпульсу (тобто ), то це буде означати врахування у спектрі цього коливання всіх складових, обмежених частотою . За формулою (7.1) знаходимо наближений вираз математичної моделі цього сигналу:

.

Якщо ж описати даний імпульс трьома рівновіддаленими відліками (тобто ), то будуть враховані всі частоти аж до 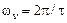й тому

.

Природно, що з ростом числа членів, що враховуються, (зі зменшенням часового інтервалу між відліками), точність апроксимації буде зростати.

Фізичний зміст цієї теореми стає зрозумілим, якщо розглянути спектри сигналів 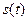та .

З рис. 7.2 видно, що містить спектр сигналу у собі спектр сигналу 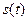і ще нескінченне число копій цього спектру, зсунутих одна відносно одної на частоту дискретизації . Якщо пропустити сигнал через фільтр нижніх частот (ФНЧ), на його виході залишиться тільки , тобто відновиться вихідний сигнал .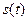

При 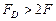копії не перетинаються з основним пелюстком спектра і таке відновлення можливе.

Якщо , копії стикаються з основним пелюстком, однак виділення вихідного сигналу 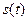ще можливе за допомогою ідеального фільтру нижніх частот із нескінченною крутизною спаду амплітудно-частотної характеристики. В іншому випадку пелюстки спектра перекриваються і відновлення вихідного сигналу 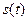неможливе. На практиці частоту завжди вибирають більшою, ніж .

Рис. 7.2. Пояснення фізичного змісту теореми Котельникова

Спектр реального сигналу рідко має точну верхню границю. Найчастіше зменшується з ростом частоти, асимптотично наближуючись до нуля.

У такому випадку на вході дискретизуючого пристрою розміщують ФНЧ з частотою зрізу, рівній ефективній ширині спектра вихідного аналогового сигналу. Його призначення – забрати залишки спектра за межами і тим самим виключити перекриття пелюстків спектра.

Date: 2016-05-25; view: 447; Нарушение авторских прав