Электростатикалық өріс. Электр өрісінің кернеулігі

Электр өрісі – электр зарядтары өзара әсерлесетін материяның түрі. Электр өрісін заряд туғызады. Қозғалмайтын заряд өрісін – электростатикалық деп атайды. Элекр өрісін өлшеуіш құралдармен байқауға болады. Осы сыншы зарядты электр өрісіне қойған кезде оң зарядтардың кеңістіктегі орнына және мәніне ешбір өзгеріс енгізбеу керек. Осыған қандайда бір F күші әсер етсін делік. Осы күштің сынақ зарядқа қатынасының векторлық шамасы электр өрісінің кернеулігі деп аталды.

Зарядтардың арасындағы әсер электр өрісі арқылы жүзеге асырылады. Кез-келген заряд өзінің айналасында кеңістіктің қасиетін өзгертеді - онда электр өрісін туғызады. Берілген жерде өрістің барын анықтау үщін ол жерге зарядталған денені орналастырып, ол электр күштерінің әсерін байқай ма жоқ па соны анықтаймыз.

Сөйтіп, электр өрісін біліп, зерттеу үшін белгілі бір “сынақ” зарядты пайдалану керек.

- бұл векторлық шаманы берілген нүктедегі (яғни сынақ зарядтың f күштің әсеріне ұшырайтын нүктедегі) электр өрісінің кернеулігі деп атайды.

Электр өрісінің кернеулігінің өлшем бірлігі: Ньютон бөлінген Кулон (Н/Кл).

4. Өрістердің суперпозициясы. Диполь өрісі.

Электр өрісінің суперпозиция (беттесу) принципі былай тұжырымдалады: Зарядтар системасының өріс кернеулігі системаның әрбір зарядтары жеке-жеке туғызатын өріс кернеуліктерінің векторлық қосындысына тең:

Бұл өрнек электростатикалық өрістің суперпозиция принципі деп аталады.

Электрлік диполь деп шамалары жағынан тең, система өрісі анықталатын нүктеге қарағанда ара қашықтығы l едәуір аз әр текті екі, +q және –q нүктелік зарядтан құрылған жүйені айтамыз.

q^- q⁺

- + (1-сурет)

Зарядтардың екеуі арқылы өтетін түзу дипольдің осі деп аталады.

Кез келген нүктедегі дипольдің өріс кернеулігі мынадай формула арқылы анықталады:

Мұндағы 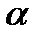- дипольдің осі мен берілген нүкте бағытының арасындағы бұрыш.

Диполь моменті деп - оң зарядтар шамасының зарядтар ара қашықтығына көбейтіндісін және диполь иінінің бағытымен бағыттас векторды айтады:

Диполь өрісінің кернеулігінің формуласы: .

5. Кернеулік векторының ағыны.

Кернеулік сызығының ағыны – скалярлы шама. Сонымен, кернеулік ағыны деп – белгілі бір бет арқылы өтетін күш сызықтарының санын айтады. Е сызықтарының жиілігі Е - нің сан мәніне тең болатындай етіп таңдап алынатындықтан, Е векторына перпендикуляр ауданшаны тесіп өтетін сызықтар саны сан жағынан Е 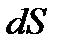-ке тең болады. Егер 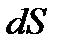ауданшасы оған түсірілген нормаль Е векторымен бұрышын жасайтындай етіп бағдарланған болса, онда ауданшаны тесіп өтетін сызықтар саны сан жағынан мынаған тең болады: Е 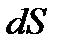. Мұндағы 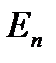- ауданшаға түсірілген нормаль бойындағы Е вектордың құраушысы.

Е (кернеулік) вектор ағыны мынаған тең: .

6. Гаусс теоремасы.

Кез келген r радиусты сфералық бетті қиып өтетін сызықтардың толық саны N сызықтар жиілігі мен сфералық бет ауданының көбейтіндісіне тең болады. Шарт бойынша сызықтар жиілігі сан жағынан шамасына тең. Демек, N шамасы сан жағынан мынаған тең:

,

яғни зарядтан кез келген қашықтықтағы сызық саны бірдей болады.

Е 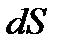өрнегіне сәйкес қандай да бір бет арқылы өтетін Е вектор ағыны сан жағынан осы бетті қиып өтетін Е сызық санына тең болады. Демек, зарядты қоршаған сфералық бет арқылы өткен Е вектор ағыны / - ге тең. Ағынның таңбасына дәл келеді. Егер бет тұйықталған және оның ішінде q заряд бар болса, кез келген басқа формалы бет үшін де Е вектор ағыны / болады.

Оны мына суреттен көруге болады:

(а) (б)

2 – сурет.

“Әжімі” (“қыртысы”) жоқ бет үшін бұл тұжырым өзінен-өзі айқын. Шынында, мұндай бет сфералық бет сияқты. Әрбір Е сызығымен бір-бір реттен қиылысады. Сондықтан қиылысу саны зарядтан шығатын сызықтардың санына, яғни / -ге тең.

“Әжімі” бар бет арқылы өтетін ағынды есептеуде ( / санды Е сызығының біреуі ғана көрсетілген 2 б–сурет), берілген Е сызығының қиылысу саны қарастырылып отырған жағдай үшін тек қана тақ болатындығын, сонымен бірге бұл қиылысулар жалпы ағынға бірде оң, бірде теріс үлесін алма-кезек қосып отыратындығын ескеру керек. Нәтижесінде берілген сызық қанша рет қиып өтпесін, ағынға қосылатын қорытынды үлес не плюс бірге (ақырында сыртқа шығатын сызықтар үшін) не минус бірге (ішке кіретін сызықтар үшін) тең болады.

Гаусс теоремасының тұжырымдамасы: тұйықталған бет арқылы өтетін электр өрісі кернеулігінің вектор ағыны осы беттің ішінде жатқан зарядтардың алгебралық қосындысын - ге бөлгенге тең.

Гаусс теоремасы былай өрнектеледі:

.

Date: 2016-05-25; view: 4673; Нарушение авторских прав