Дисперсия. Виды дисперсий

Дисперсия ( ) - средняя из квадратов отклоне­ний вариантов значений признака от их средней величины:

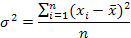
Или 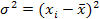для не сгруппированных данных,

для сгруппированных данных.

Свойства дисперсии.

1. Дисперсия постоянной величины равна 0.

2. Уменьшение всех значений признака на одну и ту же величину не изменяет величину дисперсии:

3. Уменьшение всех значений признака в к раз уменьшает дисперсию в k²раз:

4. Средний квадрат отклонений, исчисленный от среднего арифметического, всегда будет меньше среднего квадрата отклонений, исчисляемого от любой другой величины: > . Величина различия между ними вполне определенная, это квадрат разности между средней и этой условной величиной А.

Дисперсия альтернативного признака, т. е. признака, имеющего два противоположных значения. В таких случаях наличие признака обозначается единицей, а его отсутствие - нулем. Доля единиц, обладающих признаком, обозначается через р, доля остальных единиц - q= 1 - р. Средняя величина альтернативного признака:

Дисперсия альтернативного признака:

Cреднееквадратическое отклонение альтернативного признака:

Общая дисперсия измеряет вариацию признака во всей совокупности, возникающую под влиянием всех факторов. Исчисляется по формуле:

Групповые средние и дисперсии обозначим соответственно х. и о'. Внутригрупповые дисперсии показывают величину вариации, вызванную всеми признаками, кроме признака, положенного в основу группировки.

Межгрупповая дисперсия является мерой вариации признака между группами и характеризует колеблемостьгрупповых средних (Т) около общей средней (Т) (среднее квадратическое отклонение групповых средних от общей средней):

Date: 2016-05-14; view: 476; Нарушение авторских прав