
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания для моделирования
|
|
I. Определение оптимального радиуса шарика.
1. В столбец А ввести параметры эксперимента.
В ячейку А 1 ввести заголовок «ρ, кг/м3» (плотность шарика).
В ячейку А 2 ввести значение 7800.
В ячейку А 3 ввести заголовок «ρж, кг/м3» (плотность жидкости).
В ячейку А 4 ввести значение 960.
В ячейку А 5 ввести заголовок «η, Па·с» (коэффициент вязкости). В ячейку А 6 ввести значение1.
В ячейку А 7 ввести заголовок «R, м» (радиус сосуда). В ячейку А 8 ввести значение 0,015.
В ячейку А 9 ввести заголовок «h, м» (высота сосуда).
В ячейку А 10 ввести значение 0,3.
В ячейку А 11 ввести заголовок «g, м/с2», (ускорение свободного падения).
В ячейку А 12 ввести значение 9,81.
2. В столбец В, начиная с ячейки В2, ввести значения радиуса шарика r = 0,5–3,5 мм с интервалом 0,5 мм. В ячейку В1 ввести заголовок «r, мм» (радиус сосуда).
3. В ячейку С 1 ввести заголовок «vр» (скорость равномерного движения шарика).
Рассчитать скорость равномерного движения шарика в жидкости по формуле:
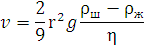
и отобразить в столбце С.
4. В столбец D ввести значения поправки, связанной с наличием стенок сосуда. В ячейку D1 ввести заголовок «k1». В ячейку D2 ввести формулу для расчета поправки:

Скопировать формулу на ячейки D 3– D 8.
5. Рассчитать относительную погрешность, связанную с поправкой, учитывающей влияние стенок сосуда, по формуле:
δ1 = (k1 − 1)⋅100%.
В ячейку Е 1 ввести заголовок «δ1» В ячейку Е 2 ввести формулу.
Скопировать формулу на ячейки Е 3– Е 8.
6. Рассчитать поправку, связанную с конечной высотой сосуда, по формуле:

и ввести результаты в столбец F.
В ячейку F1 ввести заголовок «k2».
В ячейку F2 ввести формулу.
Скопировать формулу на ячейки F3–F8.
7. Рассчитать относительную погрешность, связанную с наличием поправки, учитывающей конечную высоту сосуда, по формуле:
δ2 = (1 − k2)⋅100%
В ячейку G1 ввести заголовок «δ2» В ячейку G2 ввести формулу.
Скопировать формулу на ячейки G3–G8.
8. Рассчитать относительную погрешность, связанную с наличием обеих поправок по формуле:
δ = (1 − k1·k2)⋅100%
В ячейку Н 1 ввести заголовок «δ» В ячейку Н 2 ввести формулу.
Скопировать формулу на ячейки H3–H8.
9. Рассчитать относительную погрешность, связанную с погрешностью измерения радиуса шарика:
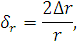
где ∆r = 0,005 мм – погрешность микрометра.
В ячейку I1 ввести заголовок «δr» В ячейку I2 ввести формулу.
Скопировать формулу на ячейки I3–I8.
10. Оформить и распечатать таблицу (табл. 1).
Таблица 1.1
| ρ,кг/м3 | r,мм | vр | k 1 | δ1 | k 2 | δ2 | δ | δr |
| ρж,кг/м3 | ||||||||
| η,Па·с | ||||||||
| R,м | ||||||||
| h,м | ||||||||
| g,м/с2 | ||||||||
11. Сделать вывод.
II. Моделирование движения шарика в вязкой жидкости при установлении режима равномерного движения.
1. Ввести заголовки столбцов в первой строке.
В ячейку А1 ввести N шага (номер шага).
В ячейку В1 ввести t (текущее время).
В ячейку С1 ввести v (скорость).
В ячейку D1 ввести δ _ v (отклонение текущего значения скорости от скорости равномерного движения).
В ячейку E1 ввести S (пройденный путь).
В ячейку F1 ввести a (ускорение).
2. Ввести значения параметров эксперимента в столбцы H и I, подписав каждый:
В ячейку H2 ввести g, м / с 2 (ускорение свободного падения).
В ячейку I2 ввести 9,8.
В ячейку H3 ввести r, м (радиус шарика).
В ячейку I3 ввести 0,001.
В ячейку H4 ввести η, Па⋅с (вязкость жидкости).
В ячейку I4 ввести 1.
В ячейку H5 ввести ρш , кг / м 3 (плотность шарика).
В ячейку I5 ввести 7800.
В ячейку H6 ввести ρж , кг / м 3 (плотность жидкости).
В ячейку I6 ввести 960.
В ячейку H7 ввести h, м (расстояние, пройденное шариком в воздухе).
В ячейку I7 ввести 0.
В ячейку H8 ввести ∆ t, с (шаг по времени).
В ячейку I8 ввести 0,001
3. Ввести параметры движения шарика:
В ячейку H9 ввести α (коэффициент,  ).
).
В ячейку I9 ввести формулу для расчета α.
В ячейку H10 ввести β (коэффициент,  ).
).
В ячейку I10 ввести формулу для расчета β.
В ячейку H11 ввести v 0 (начальная скорость).
В ячейку I11 ввести значение скорости, приобретенной шариком за время падения в воздухе, и рассчитанное по формуле  .
.
В ячейку H12 ввести v р (скорость установившегося равномерного движения).
В ячейку I12 ввести формулу для расчета скорости равномерного движения  .
.
4. Во вторую строку ввести начальные условия.
В ячейку В2 ввести 0 (начальный момент времени).
В ячейку Е2 ввести 0 (начальная координата).
В ячейку C2 ввести ссылку на начальную скорость, рассчитанную ранее.
5. Ввести формулу a =α – β*v для расчета ускорения в ячейку F2.
6. Ввести формулы для расчета времени, пройденного пути и скорости.
В ячейку В 3 ввести цепочку символов: =B2+$I$8.
В ячейку C3 ввести цепочку символов: =C2+F2*$I$8.
В ячейку D3 ввести цепочку символов: =ОКРУГЛ(C3-I$12;6)разность текущего значения скорости и скорости равномерного движения.
В ячейку E3 ввести цепочку символов: =E2+C2*$I$8.
7. Пронумеровать шаги расчета: в ячейку А 2 и последующие ввести значения, начиная с 0, с шагом 1. Количество шагов выбрать для начала 10.
Скопировать формулы из ячеек В 3, D3, С 3, E3, F2 на соответствующие нижележащие ячейки.
Затем увеличивать число шагов, пока в столбце D появятся нулевые значения при решении задачи.
8. Определить для заданных параметров:
- начальную скорость движения шарика;
- скорость равномерного движения шарика;
- характер движения до того, как оно станет равномерным; время неравномерного движения (время установления режима равномерного движения);
- расстояние, которое проходит шарик прежде, чем его движение станет равномерным;
- количество шагов вычисления, которые необходимо выполнить.
9. Исследовать, как влияет размер шарика на параметры движения.
Установить последовательно значения r = 0,0015; 0,0017; 0,002; 0,0025; 0,003; 0,0035 м. Для каждого значения r определить параметры движения так, как это делали в п. 8. Значения ∆ t каждый раз подбирать так, чтобы число шагов было минимальным, а результаты оставались корректными. Как изменяется с увлечением (уменьшением) радиуса скорость установившегося равномерного движения, время и расстояние, пройденные до этого, характер движения.
10. Исследовать, как изменяется параметры движения шарика в зависимости от начальной скорости шарика. Для этого изменяем значение h – высоты, с которой шарик падает в жидкость (радиус устанавливается в исходное положение). Задавая значения h = 0,05 - 0,2 (м) с интервалом 0,05; определить характеристики движения, приведенные в п. 8. Как изменяется с увеличением расстояния, а значит и начальной скорости, характер движения, скорость равномерного движения, время и путь при неравномерном движении? При необходимости изменить значение ∆ t.
11. Оформить результаты в виде таблицы (таблиц) согласно пункту 8 с учетом пунктов 9, 10 и сделать вывод.
Контрольные вопросы
1. Дайте определение вязкости жидкости?
2. Что влияет на точность измерения скорости?
3. Как влияет размер шарика на параметры движения?
4. Как влияет высота падения шарика на параметры движения?
Date: 2016-05-25; view: 481; Нарушение авторских прав