Определение силы (тесноты) и направления связи

Если бы существовала функциональная (математически точная) положительная зависимость между числом рабочих и доходом, т.е. если бы на каждом предприятии каждый рабочий за год производил в точности одинаковое количество продукции, все точки-объекты расположились бы на «растущей» прямой.

В этом случае, чем больше значения одного признака, тем больше значения другого и чем меньше значения одного признака, тем меньше значения другого.

Пример положительной функциональной связи между признаками X и Y изображён на рис. 4.

Рис. 4. Положительная функциональная связь

Однако на практике мы встречаемся не с функциональными, а со статистическим связями (действительно, эффективность труда, т.е. количество продукции, произведенной одним рабочим, различается на разных предприятиях). Поэтому на графике точки - объекты не лежат на одной прямой, и какую бы прямую мы ни провели, все точки на нее не попадут.

В случае положительной статистической связи мы видим "облако" точек, о котором можно сказать, что оно вытянуто по диагонали от левого нижнего угла к правому верхнему, т.е. с ростом одного признака другой в среднем растет.

Значит, и в этом случае, чем больше значения одного признака, тем больше значения другого и чем меньше значения одного признака, тем меньше значения другого. Однако это верно не для каждого объекта, а для статистической совокупности.

Пример положительной статистической связи между признаками X и Y представлен на рис. 5.

Рис. 5. Положительная статистическая связь

Если бы между признаками существовала функциональная отрицательная (а не положительная) зависимость, точки на диаграмме также расположились бы на одной прямой, однако эта прямая проходила бы в противоположном направлении.

В этом случае, чем больше значения одного признака, тем меньше значения другого и чем меньше значения одного признака, тем больше значения другого.

Пример отрицательной функциональной связи между - признаками X и Y изображен функциональная связь на рис. 6.

Рис. 6. Отрицательная функциональная связь

Аналогично для отрицательной статистической связи.

Какова бы ни была конфигурация облака точек на диаграмме рассеяния – лежат ли они в точности на одной прямой, или разбросаны хаотически – любая статистическая программа всегда сможет построить уравнение регрессии. Однако в первом случае (точки лежат на одной прямой) оно будет весьма достоверным, а во втором (точки разбросаны хаотически) – нет.

Более того, может оказаться, что через два облака, различающихся степенью близости к линейной конфигурации, будут проведены одинаковые линии регрессии.

Тем не менее зависимость между двумя переменными может иметь различный характер даже при одинаковых линиях регрессии.

Оказывается форма связи (линия регрессии) сама по себе не дает ответа на вопрос о тесноте (силе) связи пары переменных.

На этот вопрос отвечает коэффициент парной корреляции. Он показывает, насколько тесно две переменные связаны между собой.

Визуально о силе связи можно судить по тому, насколько тесно расположены точки-объекты около линии регрессии. Чем ближе точки к линии регрессии, тем сильнее связь.

Коэффициент парной корреляции r принимает значения в диапазоне от –1 до +1.

Положительные значения коэффициента корреляции r (рис. 7) свидетельствуют о положительной связи (а) между признаками, отрицательные – об отрицательной связи (б).

а)

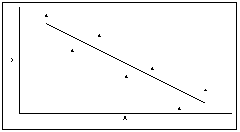
б)

Рис. 7. Направление связи

Если r = 1, то между двумя переменными существует функциональная положительная линейная связь (рис. 8), т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с положительным наклоном.

Если r = –1, то между двумя переменными существует функциональная отрицательная линейная зависимость, равен единице т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с отрицательным наклоном.

Рис. 8. Коэффициент корреляции

Если r = 0 (рис. 9), то рассматриваемые переменные линейно независимы, т.е. на диаграмме рассеяния облако точек "вытянуто по горизонтали".

Рис. 9. Коэффициент корреляции равен нулю

Date: 2016-05-25; view: 395; Нарушение авторских прав