Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей

Выделим в электрической цепи одну ветвь 2—2 с сопротивлением , присоединенную в точках 1—1 к активному двухполюснику (рис. 2-28). Покажем, что для расчета тока в ветви 2—2 активный двухполюсник можно заменить источником э. д. с. и пассивным двухполюсником. Чтобы найти э. д. с. источника, разомкнем цепь между точками 1 и 2 (рис. 2-29, а) и определим разность потенциалов опытным или расчетным путем.

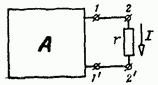
Рис. 2-28.

Затем подключим к точкам 1 и 2 источник с направленной навстречу (рис. 2-29, б); ток в ветви 2—2 останется равным нулю, так как при этом разность потенциалов любых двух точек не изменилась. Схема, показанная на рис. 2-29, б, отличается от заданной (рис, 2-28} тем,

что в ней между точками 1 и 2 включен источник и ток в ветви 2—2 равен нулю. Эта схема будет эквивалентна заданной, если между точками 1 и 2 ввести еще одну противоположно направленную э. д, с. (рис. 2-29, в).

По принципу наложения ток в ветви 2—2 эквивалентной схемы (рис. 2-29, в), а значит и заданной (рис. 2-28), найдем как алгебраическую сумму токов, создаваемых каждым из источников. Но все источники, находящиеся внутри активного двухполюсника, совместно с источником не вызывают тока в ветви 2—2 (рис. 2-29, б).

Рис. 2-29.

Поэтому ток в ветви 2—2, создаваемый одним источником (рис. 2-29, г), равен действительному току в этой ветви (рис. 2-28):

где r(в) — входное сопротивление пассивного двухполюсника, получающегося из заданного активного после того, как все э. д. с. источников напряжения и все токи источников тока приняты равными нулю.

В частности, при т. е. при коротком замыкании ветви т. е. входное сопротивление активного двухполюсника можно определить как отношение напряжения холостого Хода к току короткого замыкания:

Формулу (2-56) можно еще записать так:

(2-56а)

Последнее выражение легко получить и из (2-49). Действительно, опуская индексы у напряжения и тока, запишем это уравнение

в следующем виде:

откуда и получается (2-56а).

Сопротивление в общем случае может быть входным сопротивлением пассивного двухполюсника, присоединенного к зажимам заданного активного двухполюсника.

Уравнение (2-56) представляет собой математическое выражение теоремы об активном двухполюснике, называемой также теоремой об эквивалентном генераторе или теоремой Гельмгольца и Тевенена. Эту теорему можно формулировать следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с э. д. с. равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.

Уравнению (2-56) соответствует эквивалентная схема, показанная на рис. 2-29, д, где активный двухполюсник представлен в простейшей форме, в виде неразветвленной цепи с источником и сопротивлением. Таким образом, активный двухполюсник по отношению к присоединенной ветви с сопротивлением можно рассматривать как источник с внутренним сопротивлением равной напряжению между зажимами двухполюсника при разомкнутой ветви

Активный двухполюсник можно также представить в виде источника тока и параллельно ему присоединенного сопротивления как это показано в § 1-2.

Если рассматриваемая ветвь содержит не только сопротивление, но и э. д. с., то ток в этой ветви

где э. д. с. Е берется с положительным знаком, когда обе и Е действуют в одном и том же направлении (рис. 2-29, е), и с отрицательным, когда э. д. с. Е направлена навстречу

В дальнейшем будем называть эту теорему только теоремой об активном двухполюснике, так как при и отрицательном знаке в формуле (2-57) двухполюсник будет не отдавать, а потреблять энергию (от источника с э. д. с. Е).

Подчеркнем, что в эквивалентной схеме активного двухполюсника (рис. 2-29, д), так же как при любых других преобразованиях схем с источниками энергии, мощность источника с эквивалентной э. д. с. и потери в сопротивлении в общем случае не равны соответственно суммарной мощности источников энергии в реальной цепи и потерям в сопротивлениях ветвей активного двухполюсника.

Остановимся теперь на применении теоремы об активном двухполюснике и принципа наложения для расчета разветвленных электрических цепей.

Расчет токов в заданной электрической цепи, которую можно рассматривать относительно одной из ветвей в виде активного двухполюсника (рис. 2-28), может быть упрощен, если пользоваться принципом наложения. Действительно, ток в каждой ветви активного двухполюсника можно определить путем алгебраического суммирования токов, возникающих в этой ветви при холостом ходе (рис. 2-29, а или 6) и при действии одного источника с (рис. 2-29, г).

Удачный выбор размыкаемой ветви (режим холостого хода) может значительно упростить расчетные схемы.

Рассмотрим, например, схему на рис. 2-30, в которой требуется определить токи во всех ветвях при заданных э. д. с. источников, напряжении U и сопротивлениях ветвей.

Разомкнем ветвь с сопротивлением (рис. 2-31, а) и определим ток из уравнения

и ток из уравнения

Зная токи вычислим напряжение по формуле

Затем положим и напряжение U равными нулю и включим в ветвь с сопротивлением источник с э. д. с. (рис 2-31, б) и найдем токи во всех ветвях.

Рис. 2-30.

Рис. 2-31.

Входное сопротивление двухполюсника на зажимах 1 и 3 (ветви с сопротивлением)

Токи в остальных ветвях

Токи в ветвях заданной схемы (рис. 2-30) определяются при помощи принципа наложения:

Таким образом, шесть неизвестных токов в ветвях разветвленной схемы рис. 2-30 определены путем наложения частичных токов, найденных для простых схем (рис. 2-31, а и б).

Рис. 2-32.

Рассмотрим еще один прием расчета разветвленных цепей, базирующийся на принципе наложения и на своеобразном применении теоремы об активном двухполюснике.

Пусть в схеме (рис 2-32, а) заданы э. д. с. источников и сопротивления; требуется определить токи во всех ветвях.

При одновременном размыкании первой и второй ветвей (рис. 2-32, б) токи и напряжения в полученной схеме определяются очень просто:

При одновременном включении в первую и вторую ветви источников э. д.с. равными напряжениям (рис. 2-32, в), токи в первой и во второй ветвях будут, так же как и в схеме рис. 2-32, б, равны нулю. Если теперь в первую и вторую ветви включить еще по одному источнику с направленными противоположно э. д. с. (рис. 2-33, а), то токи во всех ветвях будут такими же, как и в заданной схеме. Так как при совместном действии источников токи в первой и второй ветвях (рис. 2-32, в) равны нулю, а схема, изображенная на рис. 2-33, а, тождественна заданной, то для расчета токов в этих ветвях достаточно учесть действие источников э. д. с. (рис. 2-33, б), что непосредственно следует из принципа наложения.

Отметим, что, поскольку в схеме на рис. 2-32, в то и ток также равен нулю, т. е. в схеме рис. 2-33, б ток равен току в заданной схеме.

Рис. 2-33.

Следовательно, для определения токов достаточно произвести расчет схемы, показанной на рис. 2-33, б, например, предварительно преобразовав треугольник сопротивлений в эквивалентную звезду. Зная токи легко найти токи в схеме рис. 2-33, б и по принципу наложения определить токи

Таким образом, и в этом случае все неизвестные токи (рис. 2-32, а) определены путем наложения частичных токов, найденных для более простых схем (рис. 2-32, б и 2-33, б).

По найденным значениям токов нетрудно рассчитать остальные токи и прямо по схеме на рис. 2-32, а.

Пример 2-6. По теореме об активном двухполюснике найти выражение для тока в ветви с измерительным прибором (рис. 2-34, а), если ток источника тока мА, сопротивление Ом, сопротивление измерительного прибора Ом, а сопротивления двух противоположных плеч моста изменяются одновременно от нуля до построить график изменения тока в зависимости от сопротивления

Решение Разомкнем ветвь с измерительным прибором (рис. 2-34, б) и Найдем равные токи:

Напряжение U (рис. 23-4, б) определим из уравнения

откуда

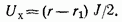
Входное сопротивление двухполюсника относительно зажимов ветви с измерительным прибором (рис. 2-34, в, без учета сопротивления)

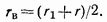
По теореме об активном двухполюснике ток

После подстановки в это выражение числовых значений получим:

На рис. 2-34, г показан график изменения тока 10 в зависимости от сопротивления. Из рисунка видно, что при изменении сопротивления ток изменяется не только по значению, но и по направлению.

Рис. 2-34.

Date: 2016-05-25; view: 923; Нарушение авторских прав