Законы и параметры магнитных цепей

1. Основные понятия и законы магнитного поля

Индукция магнитного поля В. Рассмотрим область между полюсами постоянного магнита, в которой существует магнитное поле рис. 1а. Внесём в эту область проводник с током силой I. Эффективная длина проводника в магнитном поле - l. Поместим на поверхность проводника стрелку компаса, которая расположится вдоль силовой линии поля. Ось стрелки компаса образует с осью проводника угол α. Тогда экспериментально установлено, что на проводник будет действовать сила F:

F = I ∙ l ∙B ∙ sin α. (1)

а б в

Рис. 1

В (1) коэффициент «B» называется индукцией, он является векторной величиной и силовой характеристикой магнитного поля. Индукцию можно определить как отношение максимальной силы F_max действующую на проводник длиной l = 1 м, по которому протекает ток I = 1 A:

= (2)

Размерность индукции В ® [Тл] =

Выражение (1) можно представить в векторной форме, как векторное произведение векторов (рис. 1б):

= I [ ´ ]. (3)

Если определить вектора индукции в каждой точке пространства и построить кривую, на которой вектор индукции являться касательным к этой кривой, а его модуль будет одинаков, то такая кривая будет называться силовой линией. На рис. 1в изображено семейство силовых линий магнитного поля уединённого проводника с током, По картине силовых линий можно проводить расчёты различных параметров конкретных устройств (индуктивности, силового взаимодействия и др.)

Магнитный поток Ф. Рассмотрим пространство, в котором существует магнитное поле рис. 2а, выделим поверхность S и разобьём её на бесконечно малые участки dS, в которых можно считать индукцию постоянной.

а б

Рис. 2.

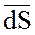= единичный вектор, перпендикулярный поверхности в данной точке.

Определим элементарный магнитный поток через элементарную поверхность dS:

dФ = dS B cos β = 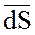- скалярное произведение векторов.

Полный магнитный поток через поверхность S, определим как потоком вектора индукции через поверхность S:

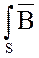
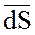Ф = dS cos β = (4)

Размерность магнитного потока Ф ® [Вебер] = [Вб] = [B c]

Рассмотрим пространство, в котором магнитный поток распределён равномерно с индукцией В рис. 2б. Поместим прямоугольную рамку с площадью S₁ под углом β к магнитному потоку, т. е. вектору . Определим магнитный поток, пронизывающий рамку:

Ф = 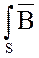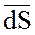= dS cos β = B cos β = B cos β S₁. (5)

Если расположить рамку, с площадью S = S₁ cos β, перпендикулярно магнитному потоку, как показано на рис. 2б, то магнитный поток через такую поверхность определится соотношением:

Ф = B S. (6)

Принцип непрерывности магнитного потока. Экспериментально установлено, что полный магнитный поток через замкнутую поверхность S равен нулю т. е.

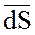= = 0 (7)

Соотношение (5) представляет фундаментальный закон магнитостатики – принцип непрерывности магнитного потока.

Напряжённость магнитного поля H. Экспериментальным путём установлено, что в магнитном поле между током i и индукцией B существует простое соотношение:

= μ_a i _∑, (8)

где - элементарный вектор касательный к линии контура L.

В (8) контурный интеграл является циркуляцией вектора вдоль замкнутого контура L, который пропорционален сумме токов i _∑ сцепленных с контуром L, охватывающим поверхность S (рис. 2а). μ_a – коэффициент пропорциональности называется абсолютной магнитной проницаемостью вещества и характеризует его физические свойства. Для однородной анизотропной среды выражение (8) можно преобразовать и получить одно из фундаментальных положений магнитостатики:

Закон полного тока:

= = i _∑, (9)

где = - напряженность магнитного поля, размерность H ® [A/м],

μ_a = μ_r μ₀ - абсолютная магнитная проницаемость вещества,

μ_r - относительная магнитная проницаемость вещества,

μ₀ - магнитная проницаемость воздуха μ₀ = 4 π 10 ^-7 Гн/м.

Закон полного тока формулируется следующим образом: циркуляция вектора напряжённости вдоль замкнутого контура L, охватывающего поверхность S, равна алгебраической сумме токов пронизывающих поверхность S(сцепленных с контуром L) (рис. 2а).

Соотношение между индукцией и напряжённостью магнитного поля можно представить в виде: = μ_r μ₀, = μ_a (10)

По магнитным свойствам все вещества подразделяются на четыре вида:

· μ_r = 1 – немагнитные вещества (вакуум)

· μ_r > 1 – парамагнитные вещества (платина μ_r = 1.0007)

· μ_r < 1 – диамагнитные вещества (висмут μ_r = 0.983)

· μ_r >> 1 – ферромагнитные вещества (железо μ_r» 1000)

Относительная магнитная проницаемость вещества показывает во сколько раз индукция магнитного поля в веществе больше чем в вакууме.

Кривая намагничивания вещества.

Особый интерес в электротехнике представляет использование ферромагнитных веществ – электротехнических сталей, которые позволяют сконцентрировать основной магнитный поток внутри стальных участков устройства, так называемого магнитопровода.

УРОК № 6

Date: 2016-05-25; view: 703; Нарушение авторских прав