Расчет дебита фильтрующейся жидкости для различных видов пористости

Оценка дебита жидкости при линейном режиме равномерной фильтрации

Теория к разделу

Рассмотрим случай субкапиллярной фильтрации, т.е. фильтрация равномерная и проходит через всю площадь образца, имеющего субкапиллярную пористость.

Дебит жидкости при линейном режиме оценивается уравнением Дарси:

, (3.1)

где k_пр – проницаемость, Д;

F – площадь фильтрации, см²;

∆P – перепад давления, атм;

m – вязкость, спз;

L – длина, см.

Типовая задача

Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мД, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. Определить дебит жидкости.

Дано:

k_пр = 10 мД = 0,01 Д;

F = 100 см²;

∆P/L = 0,25 атм/м = 0,0025 атм/см;

m = 1 спз.

Найти: Q₁

Решение:

,

.

Оценка дебита жидкости при неравномерно-проницаемой фильтрации

Теория к разделу

Проницаемость жидкости при фильтрации через капилляр оцениваем из соотношения уравнений Дарси:

(3.2)

и Пуазейля:

, (3.3)

откуда:

, (3.4)

где k_пр.кап – проницаемость при фильтрации жидкости через капилляр, Д;

F – площадь фильтрации, см²;

∆P – перепад давления, атм;

m – вязкость, спз;

L – длина, см.

После преобразования коэффициента проницаемости и радиуса капилляра к одной размерности получим эмпирическое уравнение для оценки коэффициента проницаемости при фильтрации жидкости через капилляр:

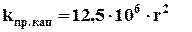. (3.5)

Типовая задача

Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мДарси, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. В этом кубике существует один капилляр диаметром 0,2 мм. На сколько увеличится суммарный дебит при прочих равных параметрах m и ∆P/L?

Дано:

D_к = 0,2 мм = 0,02 см;

∆P/L = 0,25 атм/м = 0,0025 атм/см;

m = 1 спз;

N_к =1.

Найти: Q₂ - дебит при фильтрации через капилляр;

Q₃ - суммарный дебит за счёт субкапиллярной и капиллярной фильтрации.

Решение:

,

,

.

Рассчитаем дебит через этот капилляр:

,

.

По сравнению с субкапиллярной проницаемостью (k_пр = 10 мД) дебит увеличится при наличии одного такого канала на 40% (Q₂ / Q₁), а если бы субкапиллярная проницаемость была k_пр = 1 мД, то дебит увеличился бы на 400% (Q₂ / Q₁ × k_пр).

Date: 2016-05-24; view: 1998; Нарушение авторских прав