
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Занятие 3. Расчет волновых параметров ДЭП СВН
|
|
Задача3.1
Удельные параметры линии 750 кВ с проводами 4х(АС 400/93) следующие: r 0 = 0,018 Ом/км; x 0 = 0,28 Ом/км; b 0 = 3,99·10-6 Cм/км.
Среднегодовые потери на корону для этой линии составляют Δ P к = 12,3 кВт/км.
Требуется: найти волновые параметры линии для двух случаев - для реальной линии с учетом потерь и для идеализированной линии.
Решение.
Коэффициент распространения волны для реальной линии определяется выражением
 .
.
Входящая в это выражение величина g 0 может быть определена с учетом потерь на корону
 1/(Ом·км),
1/(Ом·км),
откуда
 Коэффициент фазы
Коэффициент фазы  1/км;
1/км;
Коэффициент затухания  1/км.
1/км.
Волновое сопротивление линии равно
 Ом.
Ом.
В настоящее время потери мощности на корону учитываются не в виде распределенной проводимости g 0, а в виде сосредоточенных отборов мощности по концам линии. При этом можно принять g 0 = 0. Для этого случая волновые параметры рассматриваемой линии будут иметь следующие значения:
- коэффициент фазы
 1/км;
1/км;
- коэффициент затухания
 .
.
Отсюда коэффициент распространения волны будет иметь значение
 .
.
Волновое сопротивление при g 0 = 0
 Ом.
Ом.
Для идеализированной линии будем иметь:
- коэффициент распространения волны
 1/км;
1/км;
- волновое сопротивление
 Ом.
Ом.
Результаты расчетов сведены в табл.2.2.
Таблица 2.2
| Учитываемые допущения | γ0, 1/км | α0, 1/км | β0, 1/км | z 0, Ом |
| реальная линия с учетом | 
| 1,059·10-3 | 0,037·10-3 | 
|
| реальная линия без учета | 
| 1,057·10-3 | 0,034·10-3 | 
|
| идеализированная линия | 1,057·10-3 | - | 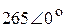
|
По сравнению с реальной линией погрешность в определении коэффициента распространения волны составляет:
- линия без учета g 0 – 0,09%;
- идеализированная линия – 0,1%.
Занятия 4-5. Расчет напряжений на ДЭП
Задача 4.1
Воздушная линия электропередачи номинального напряжения 500 кВ имеет длину 700 км и выполнена с применением фазных проводов 3х(АС 330/43), подвешенных на стальных портальных опорах с оттяжками типа ПБ-1-3, имеющих междуфазное расстояние 12,8 м. Погонные параметры линии при шаге расщепления фазы 40 см таковы: x 0 = 0,308 Ом/км, b 0 = 3,60·10-6 См/км. Волновое сопротивление z в = 292,5 Ом. Активное сопротивление одиночного провода при температуре +200С r (1)(+20) = 0,089 Ом/км.
Требуется:
1. Найти распределение напряжения, тока и реактивной мощности вдоль линии, принимаемой идеализированной, для двух характерных режимов работы, отличающихся передаваемой активной мощностью:
а) передается наибольшая возможная мощность, исходя из сохранения апериодической статической устойчивости с нормированным запасом 20%, для двух случаев:
- напряжения на концах линии равны;
- напряжение в начале линии превышает напряжение в конце в 1,12 раза (создается перепад напряжения);
б) передается мощность, составляющая 30% от натуральной мощности, при одинаковых напряжениях на концах линии.
2. Построить векторные диаграммы напряжений и токов для анализируемых режимов.
3. Оценить потери активной мощности при передаче наибольшей и наименьшей мощностей и равных напряжениях на концах линии, пользуясь значениями среднего квадратичного тока; принять, что режим передачи наибольшей мощности является зимним (средняя январская температура равна 00С), а режим передачи наименьшей мощности – летним (средняя июльская температура равна 200С).
Решение:
Максимальная мощность, которая может быть передана по линии при значениях напряжения U 1 и U 2 на ее концах, поддерживаемых неизменными, составляет
 .
.
Если принять, что U 1 = k·U 2, где k – перепад напряжения, то 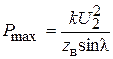 или в относительных единицах при
или в относительных единицах при  имеем
имеем  . Принимая k = 1, получим
. Принимая k = 1, получим 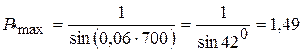 .
.
Наибольшая мощность, которую можно передать с учетом нормативного коэффициента запаса
 .
.
В рассматриваемом режиме определяем распределение напряжения по длине линии для случая U 1 = U 2. Напряжение в промежуточной точке линии x, удаленной на расстояние lx от приемного конца, выражается так
 .
.
Здесь вектор напряжения в конце линии  принимается за ось отсчета углов фазового сдвига векторов напряжения и тока, соответствующих другим промежуточным точкам линии.
принимается за ось отсчета углов фазового сдвига векторов напряжения и тока, соответствующих другим промежуточным точкам линии.
Величина реактивной мощности в конце линии Q *2 в долях от натуральной мощности вычисляется по формуле, получаемой из уравнения круговой диаграммы мощности
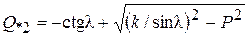 ;
;
 .
.
Поскольку линия – идеализированная и 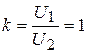 , то Q *1 = -Q *2 = + 0,29.
, то Q *1 = -Q *2 = + 0,29.
Рассматриваются несколько промежуточных точек линии, отстоящих от ее конца на расстояния равные 200, 350, 500 и 700 км. В табл. 4.1 занесем значения тригонометрических функций волновой длины.
Таблица 4.1
| lx, км | ||||
| λx = α0· l x, эл. град | ||||
| cos λx | 0,978 | 0,933 | 0,866 | 0,743 |
| sin λx | 0,208 | 0,358 | 0,5 | 0,669 |
Расчет напряжений для промежуточных точек линии
lx = 200 км
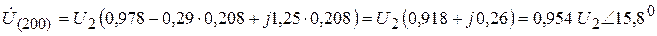
lx = 350 км (середина линии)

lx = 500 км
 ;
;
lx = 700 км
 .
.
По результатам расчетов строится эпюра распределения напряжения (рис. 4.1а). В середине линии получили минимум напряжения. Значит, на концах линии допустимо поддерживать наибольшее рабочее напряжение, назначаемое по условиям работы изоляции электрических аппаратов (см. ниже).
Такой выбор значений напряжения позволяет снизить потери активной мощности при ее передаче.

Рис. 4.1. Распределение напряжения, тока и реактивной мощности по длине линии в режиме передачи наибольшей мощности при работе без перепада напряжения
Переходим к расчетам, выполняемым с целью нахождения распределения тока в режиме передачи наибольшей мощности при k = 1.
Ток в некоторой промежуточной точке линии
 .
.
Принимая за базисный ток, соответствующий передаче натуральной мощности,
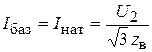 ,
,
имеем выражение для расчета токов в относительных единицах
 .
.
В конце линии электропередачи (lx = 0)
 ;
; 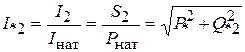 .
.
Тогда при P* = 1,25 и Q*2 = -0,29 (см. выше)
 .
.
Угол φ2 фазового сдвига вектора тока I 2 относительно напряжения U 2, вектор которого принят за ось отсчета углов,
 эл.град.
эл.град.
Следовательно, вектор тока I 2 опережает вектор напряжения U 2 на 13,1 эл.град.
Рассчитываются токи для промежуточных точек линии
lx = 200 км
 ;
;
lx = 350 км
 ;
;
lx = 500 км
 ;
;
lx = 700 км
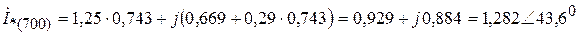 .
.
Угол  эл.град., то есть вектор тока I 1 отстает от напряжения U 1 на угол 13,10. Действительно,
эл.град., то есть вектор тока I 1 отстает от напряжения U 1 на угол 13,10. Действительно,  и разность фазных углов напряжения и тока в начале линии 56,70 - 43,60 = 13,10.
и разность фазных углов напряжения и тока в начале линии 56,70 - 43,60 = 13,10.
Строится распределение тока по линии (см. рис. 4.1б). В середине линии получили максимум тока.
Рассчитываем средний квадратичный ток
 ;
;
 .
.
Приступаем к расчетам по определению распределения реактивной мощности по длине линии
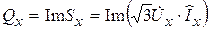 ;
;
 ;
;  ;
;  ,
,
причем S баз = P нат, так как  , а U баз = U 2 (U баз ≠ U ном в общем случае).
, а U баз = U 2 (U баз ≠ U ном в общем случае).
Расчет значений полной мощности
lx = 200 км
 ;
;
lx = 350 км (середина линии)
 ;
;
lx = 500 км
 ;
;
lx = 700 км
 ;
;
lx = 0; Q *2 = -0,29; Q *1 = +0,29.
Эпюра реактивной мощности показана на рис. 4.1в. По результатам вышеприведенных расчетов строится векторная диаграмма напряжений и токов для режима наибольшей передаваемой мощности (рис. 4.2).

Рис. 4.2. Векторная диаграмма напряжений и токов для режима передачи наибольшей мощности при работе без перепада напряжения
Сделаем оценку потерь активной мощности в рассматриваемом режиме, принимая U 1 = U 2 = U нбр = 1,05 U ном = 525 кВ
 МВт;
МВт; 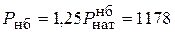 МВт;
МВт;
 кА;
кА;  кА.
кА.
При средней январской температуре t ср.ян = 00С погонное активное сопротивление провода АС 330/43 составляет
 Ом/км.
Ом/км.
Трехфазные потери активной мощности
 МВт;
МВт;  .
.
Режим наименьшей передаваемой мощности.
Реактивная мощность в конце линии
 .
.
Расчет напряжений для промежуточных точек линии
lx = 200 км
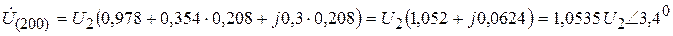 lx = 350 км (середина линии)
lx = 350 км (середина линии)
 lx = 500 км
lx = 500 км
 ;
;
lx = 700 км
 Строится распределение напряжения вдоль линии (см. рис. 1.7а). В середине линии получился максимум напряжения.
Строится распределение напряжения вдоль линии (см. рис. 1.7а). В середине линии получился максимум напряжения.

Рис. 4.3. Распределение напряжения, тока и реактивной мощности
по длине в режиме передачи наименьшей мощности
Повышение напряжения в промежуточных точках линии ограничивается величиной U длд с целью исключения общего коронирования проводов. В долях от номинального напряжения линии
 .
.
Для проводов 3х(АС 330/43) при шаге расщепления 40 см, относительной плотности воздуха δ ≥ 1,00 и D = 12,8 м U длд > 1,065. Поэтому в рассматриваемом режиме по концам ВЛ допустимо поддерживать напряжение выше номинального. Однако, учитывая, что реактивная мощность Q *2 существенно возросла по сравнению с режимом наибольшей передаваемой мощности и изменила свой знак (стекает с линии), может потребоваться установка дополнительных компенсирующих устройств (шунтирующих реакторов) для ее потребления. Ввиду этого принимаем U 1 = U 2 = U ном. Тогда
 МВт.
МВт.
Расчеты для построения распределения тока по линии
 кА.
кА.
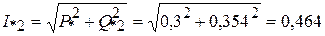 ;
;
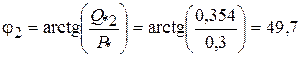 эл. град., т.е. вектор тока I 2 отстает от вектора напряжения U 2 на угол 49,7 эл. град.
эл. град., т.е. вектор тока I 2 отстает от вектора напряжения U 2 на угол 49,7 эл. град.
lx = 200 км
 ;
;
lx = 350 км
 ;
;
lx = 500 км
 ;
;
lx = 700 км
 .
.
Распределение тока показано на рис. 1.7б.
Угол φ2 = -φ2 = -49,7 эл.град. (ток I 1 опережает напряжение  . Разность фазных углов тока I 1 и напряжения
. Разность фазных углов тока I 1 и напряжения 
61,22 – 11,5 = 49,72 эл.град.
Векторная диаграмма напряжений и токов при наименьшей передаваемой мощности приведена на рис. 4.4.

Рис. 4.4. Векторная диаграмма напряжений и токов для режима передачи наименьшей мощности
Расчеты для построения распределения реактивной мощности (см. рис. 1.7в):
lx = 200 км
 ;
;
lx = 350 км
 ;
;
lx = 500 км
 ;
;
lx = 700 км
 .
.
Ниже оцениваются потери активной мощности при передаче P *нм = 0,3:
 кА;
кА;
 МВт;
МВт;
 %.
%.
Режим наибольшей передаваемой мощности при перепаде напряжения k = 1,12.
Реактивная мощность в конце ВЛ при P * = 1,25
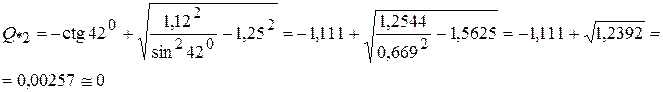 Реактивная мощность в начале ВЛ
Реактивная мощность в начале ВЛ
 .
.
Поскольку Q *2 = 0, реактивная мощность, поступающая в начало линии, расходуется на покрытие разницы между потерями и генерацией этой мощности (Δ QL > Δ QC). Распределение режимных параметров по длине ВЛ будет существенно иным, чем в том же режиме, но без перепада напряжения (см. табл. 4.2).
Таблица 4.2
| lx, км | |||||

| 1,00Ð00 | 1,012Ð14,90 | 1,035Ð25,60 | 1,068Ð35,80 | 1,119Ð48,40 |

| 1,25Ð00 | 1,24Ð9,70 | 1,22Ð17,10 | 1,192Ð24,80 | 1,119Ð48,40 |
| Q * x | 0,1137 | 0,1866 | 0,2429 | 0,280 |
Напряжение в начале линии не может превышать U нбр = 1,05 U ном, тогда можно определить U 2, если U 1 = 525 кВ:
 кВ.
кВ.
Натуральная мощность при этом будет
 МВт.
МВт.
Объяснение полученных результатов (см. табл. 4.2). Хотя в конце линии Q 2 = 0 и полная мощность S 2 = P 2 меньше, чем полная мощность в начале  > 1,25, но из-за того, что U 1 > U 2, ток в начале линии оказывается меньшим, чем в конце. Распределения режимных параметров даны на рис. 4.5. Векторная диаграмма изображена на рис. 4.6. Ее отличием от предыдущих случаев является совпадение по фазе векторов напряжения и тока в конце линии.
> 1,25, но из-за того, что U 1 > U 2, ток в начале линии оказывается меньшим, чем в конце. Распределения режимных параметров даны на рис. 4.5. Векторная диаграмма изображена на рис. 4.6. Ее отличием от предыдущих случаев является совпадение по фазе векторов напряжения и тока в конце линии.

Рис. 4.5. Распределение напряжения, тока и реактивной мощности
по длине в режиме передачи наибольшей мощности при работе
с перепадом напряжения k = 1,12

Рис. 4.6. Векторная диаграмма напряжений и токов для режима передачи наибольшей мощности при работе с перепадом напряжения k = 1,12
Date: 2016-05-24; view: 1871; Нарушение авторских прав