
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Жүйенің істен шығу ықтималдылығының» анықтамасы
|
|
Қалпына келмейтін жүйе кезінде(паралель) элементтің қосылуы (5.2 суретте) және міндеті, паралель бір элементтердің қосылуы кезінде системаның жұмыс істеуі және барлық паралель элементтің қосылуы кезінде жүйенің істен шығуы керек. Егер паралель қосылған элементтердің қосылмауы және ықтималдықтың істен шығуы:
Q c(t) = Q 1(t) Q 2(t) ....Q m-1(t) Q m(t)= 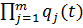 (5.2)
(5.2)
Істен шығу ықтималдығы жүйесін тоқтаусыз жұмыс істеу, яғни ықтималдығы кері болып табылады,
Q(t1)=1- P(t1); (3.3)
Q(t1)=1-  (3.4)
(3.4)
λt << 1 кезде, яғни уақыт Т кезінде, сәтсіздікке орташа уақыт әлде қайда аз t=1/l өрнек (3.2), электр қуаты сериясы кеңейту алғашқы екі шарттарын ауыстыру арқылы жеңілдетуге болады.
Істен шығу ықтималдығы: Q = 1-  (5.2)
(5.2)
8.Істен шығу қарқындылығы осы уақытқа дейін туындамаған жағдайында t уақыты сәтіндегі жүйенің тоқтап қалу ықтималдылығының шартты тығыздығы ретінде анықталынады.
Істен щыққын объектілердің қайта қалпына келтірілмеуі және олардың дұрыс жұмыс жасап тұрған объектілермен ауыстырылмау шартында уақыт бірлігіндегі тоқтап қалған объектілер санының сол уақытта дұрыс жұмыс жасап тұрған объектілердің орташа санына қатынасын білдіреді. Жүйенің жұмысқа қабілеттілігі шартындағы жүйенің аралықтағы тоқтаусыз жұмысының шартты ықтималдылығы өрнекпен анықталынады (2.7):
P(t,t+ D t) = 1- P(t+ D t)/P(t) = -[ P(t+ D t)-P(t)]/P(t) (2.7)
Уақытты нөлге бағыттап, істен шығу қарқындылығының ықтимал мәнін аламыз:
l =lim (2.8)
Істен шығу қарқындылығының статистикалық анықтамасы:
(2.9)
Істен шығу қарқындылығы l(t) тоқтаусыз жұмыс істеудің өзгеруінің көрнекі көрінісін береді. Уақытқа тәуелділік 2.3 суретте көрсетілген. Іске кірістіру кезеңінде жүйенің жекелеген элементтерін жасаудың жасырын ақаулары, құрастыру мен жөндеу кемшіліктері, тасымалдау нәтижесінде болған бұзылыстар анықталынады. Пайдалану кезеңі істен шығу қарқындылығының салыстырмалы тұрақты көрсеткішімен сипатталынады. Жүйенің тозуы кезеңінде жекелеген элементтердің тозуы мен олардың сипаттамаларының өзгерісінің әсерінен істен шығу қарқындылығы артады.
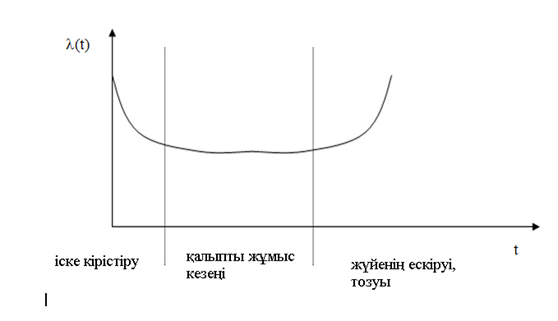 2.3 сурет. Жүйенің істен шығу қарқындылығы өзгерісінің қарапайым өзгерісі
2.3 сурет. Жүйенің істен шығу қарқындылығы өзгерісінің қарапайым өзгерісі
9.Экспоненциалды бөлу. Үзіліссіз кездейсоқ шама – жүйенің істен шығуға дейінгі пайдаланым жүйенің қасиеттері мен оның элементтеріне, жұмыс жасау жағдайларына, істен шығудың сипаты мен басқа да факторларға байланысты бөлудің әр түрлі заңдарымен сипатталына алады. Істен шығуға дейінгі пайдаланымды бөлу функциясы бар экспоненциалды (көрнекі) бөлу кеңірек таралған.
мұндағы λ - осы бөлу істен шығу қарқындылығы параметрін
тарату тығыздығына сәйкес әдетте, үздіксіз функциясы F (T),
f(t) = 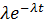 (3.2)
(3.2)
Уақытта t кезінде іркіліс пайда немесе пайда болмауына тұратын іс-шаралар, қарама-қарсы болып табылады. P (T) - Тоқтаусыз жұмыс істеу ықтималдығы. Т = 0, жүйе жедел болса, онда P (0) = 1.
Уақыт t артуына байланысты, P (T), сондықтан, 0 = жақындап және P (T) үшін монотондылық азаяды,
P(t)=  (3.2)
(3.2)
Істен шығу ықтималдығы жүйесін тоқтаусыз жұмыс істеу, яғни ықтималдығы кері болып табылады,
Q(t1)=1- P(t1); (3.3)
Q(t1)=1-  (3.4)
(3.4)
λt << 1 кезде, яғни уақыт Т кезінде, сәтсіздікке орташа уақыт әлде қайда аз t=1/l өрнек (3.2), электр қуаты сериясы кеңейту алғашқы екі шарттарын ауыстыру арқылы жеңілдетуге болады. Содан кейін, мысалы, өрнек (3.2) нысанын қабылдайды:
P(t)=1- 𝛌t=1-t/τ (3.5)
Мұнда τ-істен шығу уақытын білдіреді. Бұл қате нәтижесінде 0,5 (λt1) 2 аспайды. Экспоненциалды тарату тән бір қасиеті тән: мемлекеттік ықтималдығы P (T1, T2) аралығы (Т1, Т2) жылы кезінде t1 жүйесі жұмыс істейді, ықтималдығы P (T) аралықта ұзындығы байланысты ескертпелі (t1 - T2) және уақыт t1 жүйесін алдыңғы жұмыс, яғни байланысты оның «жасы» бастап. Олардың анықтамалары бойынша орындамағаны және дисперсия істен бағамы уақыт білдіреді:
t=1/l; (3.6)
D[T]=1/l2; (3.7)
l(t) = f(t)/P(t) = l; (3.8)
Ескере қартаю ешқандай бөлігін іске қосу-жылы кез келген кезеңін алып, киіп мүмкін емес жүйелер мен компоненттер, (көптеген компьютерлік жабдықтар, аппаратура, компоненттер мен басқару жүйелері) - экспоненциалды заңы осы заңның қолдану өрісі, істен бағамы λ = const тұрақтылық сипатталады бері. Экспоненциалды тарату ақ көптеген құрамдас бөліктерден тұратын күрделі жүйелердің үздіксіз жұмысын сипаттайды, сондықтан бұл бөлу қолдану бағалауды сенімділігі ең оңай болып табылады. P(t),f(t),l(t) 
Экспоненциалды тарату үшін сенімділік параметрлерін өзгерістер графиктері - 3.1-суретте
10.Қалыпты тарату Қалыпты айырмашылығы экспоненциалды тарату осындай жүйелер мен тозуы іс-қимыл ұшырайды әсіресе оның элементтерін сипаттау үшін қолданылады. Сонымен қатар, біз t, істен Т ескере уақыт функциясы және тарату тығыздығын қабылдауға тиіс - істен орташа уақыт.
Қалыпты үлестірімінің параметрлері болып табылады: м - кездейсоқ шаманың күту, T - жеткіліксіздігі (немесе істен) уақыт; σ - тест-жүйелер қорытындысы туралы істен Т уақыт стандартты ауытқуы.Қалыпты тарату диапазонында кездейсоқ құндылықтарды әрекетін сипаттайды (- ∞, ∞), өйткені істен шығу уақыты орнына қалыпты, негізінен қысқартылған қалыпты бөлу пайдаланылуы, бұл ескеру үшін, теріс емес.
Кездейсоқ шаманың мүмкін мәндер облысы (Т = 0 0) 0-ден ∞ дейін болуы мүмкін. М <3σ егер қысқартылған қалыпты үлестірімі, әйтпесе жеткілікті дәлдігін қамтамасыз етеді (резидент-қысқартылған) бөлу ғана қалыпты астам қолдану, қолданылады. Қалыпты үлестірімінің сенімділігін көрсеткіштері:



|
|
|




Сурет 3.2 - қалыпты бөлу сенімділік көрсеткіштерінің графиктері өзгерту.
11.Вейбулл – Гнеденко таратуы Гнеденко тиісінше, функциясын және тығыздығы бөлу сипаттайды, сенімділік теориясының қолданбаны Вейбулл алды:
 ; f(t)=αktk-1
; f(t)=αktk-1  (3.9)
(3.9)
Бұл параметр K оның шкаласы α- жеткіліксіздігі ықтималдық тығыздығы параметр түрін анықтайды екі параметр тарату болып табылады. Мысалы, К = 1, Вейбулл - Гнеденко істен шығу жылдамдық константасы кезде экспоненталық сәйкес келеді. К> 1, істен шығу жиілігі бірсарындылығы арттырады. Қашан K <1 бірсарындылығы азаяды. (сурет 3.3)
Тарату Вейбулл -Гнеденко іске қосылған-кезең, оның ішінде электрондық және механикалық аппараттық істен шығу уақытын сипаттау үшін пайдаланылуы мүмкін.


Рисунок 3.3 - Вейбулл-Гнеденкографиг көрсеткішінің сенімділігінің өзгеруі.
12.Қалпына келтiрiлетiн жүйелерінің сенімділігі көрсеткіштері
Сенімділік көрсеткіштері. Жүйені қалпына келтіру үшін, сенімділіктін түрлі көрсеткіштерін пайдалануға болады. Дискретті кездейсоқ процесс ретінде істен шығу ағыны мөлшерлемесін орнату η (t) –істен шығу интервалының саны (0, t) істен шықпау көрсеткіш параметрдің істен шығуы ώ (t), (4.1)
Орташа істен шығуы - θ, жұмыс уақыты тығыздығы f (t) бір тарату ықтималдық көрсеткіштің мынадай математикалық өрнек бар: (4.2) Қарапайым параметр ағынында істен шығу ағыны ώ, орташа істен шығуы θ=1/ώ. (4.3) Іске жарамдылық көрсеткіші. Іс жүзінде, қалпына келтіру ұзақтығы әрдайым дерлік істен шығудан айтарлықтай аз уақыт алады, бірақ көптеген сенімділігі проблемалар үшін қалпына келу ұзақтығын ескермеу мүмкін емес (мысалы, зақымдануы салдарынан шығындардың есептеу, қажетті қызмет көрсету персоналының және басқалар сомасына.). Тв кездейсоқ өлшем жүйенің жұмыс істеу қалпына келтіру ұзақтығы (қалпына келтіру уақыты бойынша).
Тв-ң тарату уақытына қалпына келтіру бойынша бірде байланысты, не алдыңғы қалпына келтіру ұзақтығы, не істен шығу арасындағы алдыңғы операциялық уақытқа тәуелсіз. Тарату функциясы өлшемі Тв көрсетеміз G(t), тарату тығыздығы g(t). Істен шығу арасындағы жұмыс уақыты біркелкі және бір-біріне тәуелсіз өлшеміне тәуелді емес болса, онда қалпына келтіру уақыт негізделген бас тарту ағыны қалпына келтіру процесін айнымалы (альтернирующего процесса) деп аталады. Бұл үдеріске, сондай-ақ қалпына келтіру үдерісіне,орташа істен шығу θ орташа істени шығу уақыты t. Кестеде берілген жүйенің жұмыс қалпына келтіру уақыты суретте көрсетілген 4.1.
ξ1=T ξ2 ξ3 ξ4tTB3TB2TB1 0 Рисунок 4.1 – Жүйенің жұмыс істеу кестесі, қалпына келтіру уақытын ескере отыра. Жұмысқа жарамды көрсеткіш, көрсетілген уақыт t1 ішінде жұмыс жағдайын, сондай-ақ ықтимал болып табылады және жөндеу үшін орьаша қалпына келу уақытын білдіреді.
G(t)= P{Tв< t1}; τв=М[Tв] (4.4) Бұл көрсеткіштердің статистикалық анықтамасы: (t1)= l(t1)/m; (4.5) Мұнда l(t1) – қалпына келу саны, ұзақтығы кіші t1; m – қалпыны келу саны; tвi – істен шыққаннан кейінгі қалпыны келу уақыты уақыты i. Беріктік көрсеткіштері. Қолданысқа түсу ұзақтығы шектеулі шекараға дейін жүйенің жұмыс атқару уақыты деп аталады. Қызмет көрсету мерзімі Тс белгіленеді кездейсоқ айнымалы болуы мүмкін. Содан кейін ұзақ көрсеткіш ретінде орташа қызмет ету мерзімін қабылдай алады
tc=M[Tc] (4.6) немесе гамма - беріледі мерзімді пайыздық tγ қызметі Р{Tc> tγ,} = γ/100. (4.7) Осыдан, tγ, - күнтізбелік уақыт аралығы қолданысқа шыққаннан кейін, осы аралықта ол шектік жағдайына жетпейді.
Бұл көрсеткішті γ = 100%, tγ ретінде түсіндіруге болады. Беріктік көрсеткіші тек қана жұмыс уақытына тәуелді емес, эксплуатации уақытынан шектік жағдайына дейін. Сенімділіктін кешенді көрсеткіштері. Сенімділік компоненттерінің бірін сипаттайды, олардың әрқайсысы қалпына келтiрiлетiн жүйелерінің сенімділік мынадай көрсеткіштермен, сонымен қатар бірлесіп сенімділігі мен жөндеуге жарамды, кешенді көрсеткіштерін пайдаланылады. Оларға мыналар жатады: дайындық коэффиценті - kг, жедел дайындық коэффициенті - kо.г(t) және техникалық пайдалану коэффициенті - kт.и..
13.Қалпына келмейтін жүйелердің сенімділік көрсеткіштері. Сенімділік көрсеткіштерін таңдағанда көрсеткіштер жүйенің сенімділігін жан-жақты, толық сиппаттауын, аналитикалық есептеулер мен сынақ нәтижелері бойыша экпеиментттік тексерулер жүргізуде ыңғайлы, дұрыс физикалық мағынасының болуын және тиімділік көрсеткіштеріне ауысу қасиеттерінің болуын ескеру қажет. Қалпы келмейтін жүйелер үшін тоқтаусыз жұмыс істеу көрсеткішімен ғана шектелуге болады. Қалпына келмейтін техникалық жүйелердің тоқтаусыз жұмыс істеуі жүйе сенімділігінің басты құрамда бөліктерінің бірі болып табылады. Себебі, ол жүйенің ұзақ уақыт істен шықпай жұмыс істей алу қабілетін көрсетеді. Жүйенің бұл қабілеті оның тиімділігіне және элементтердің саны мен тоқтаусыз жұмыс істеуіне, жұмыс істеу режимі мен көшірменің(резервтің) болуына, қоршаған ортаның параметрлеріне (температура, ылғалдылық, атмосфералық қысым және т.б.) үлкен дәрежеде әсер етеді.Тоқтаусыз жұмыс істеу көрсеткіші негізінде істен шыққаннан кейін қалпына келтіруге болатын, бірақ жұмысын бірінші істен шыққанға дейін қарастыру жөн болатын жүйелерді суреттейді. Оларыдың қатарына, мысалы, істен шығуы өте сирек және салдры өте ауыр болатын жүйелер жатады. Істен шығуға дейін жұмыс істеудің тарату тығыздығы мен функциясы. Істен шығуға дейін жұмыс істеу Т әріпімен, ал тарату функциясы, кез-келген басқа кездейсоқ шама сияқты F(t) деп белгіленеді.Тарату функциясы F(t) кездейсоқ шаманың ықтималдығы Р (тоқтаусыз жұмыс істеу ықтималдығы) ретінде анықталады. Және оның негізінде істен шығуғадейін жұмысістеу Т белгісіз-бір жұмыс істеу t (уақыт) мәнінен аз болуы жатыр.
F(t)=P{T<t} (2.1)
Бұл ықтималдық кез-келген болуы мүмкін Т шамасының барлық ауқымын алып тұрған t функциясы ретінде қарастырылады. во всем диапазоне возможных значений величины.
Кез-келген кездейсоқ шмаың тарату функциясы кемімейтін t уақыт функциясы. Уақыт шексіздікке ұмтылғанда (t→∞) F(t) бірге ұмтылады (F(t) →1).

2.2 сурет. – F(t) тарату функциясы мен сенімділік функциясының P(t) шамамен алынған көрінісі
F(t) ықтимал функцияны анықтау үшін(2.1) көрсетілгеннен басқа, барлық сенімділік көрсеткіштері үшін сенімділікке сынау кезінде қолданылатын статистикалық анықталады келтіруге болады. Статистикалық анықтамалар ықтималдық анықтамаларды толық түсіндіруге мүмкіндік береді. Ары қарай сатистикалық анықтамаларды ирек сызықпен белгілейміз.
Қалпына келмейтін жүйелердің сенімділік көрсеткіштерінің статистикалық анықтамаларын қарастыру үшін сынаққа бірдей жүйелер қойылған, сынақ шарттары бірдей, ал әр жүйе үшін сынақ істен шыққанға дейін жүргізіледі деп ойлайық. t уақытына қарай тоқта қалған жүйелер санын N(t) деп белгілейік. Сонда, (0;t) аралығында N(0)=0, ал t→∞ кезінде N(t) →N болатыны анық.
F(t) тарату функциясының статистикалық анықтамасы:
~ ~
F(t)=N(t)/N (2.2)
Таратудың сататистикалық функциясы істен шыққан кезде 1/N болатын қысқа секірістері бар баспалдақ тәрізді сызық (2.2 сурет). N сынаққа қатысытын жүйелер саны артқан сайын таратудың статистикалық функциясы ықтималтарату функциясымен теңеседі.
t уақыт кезінде істен шығуы мен техникалық жүйенің дұрыс жұмыс істеуі үйлесімді емес, сол себепті тағы бір сенімділік функциясы деп аталатын функцияны енгізейік:
P(t)=P{T>=t}=1-F(t) (2.3).
Бұл кезде t =0 болғанда жүйе жұмыс істей алады, онда Р(0)=1 болады. Сенімділік функциясының үлгісі 2.2 суретте көрсетілген.
14. істен шығуға дейінгі орташа пайдаланым (жүйенің тоқтаусыз жұмыс істеуінің орташа уақыты) – Т кездейсоқ шаманың математикалық күтімі (М[T]) - жүйенің (объектілердің) бірінші істен шығуына дейінгі пайдаланымы жатады.
¥
t = М[T]= ò t* f(t)dt; (2.10)
¥
t = òP(t)dt; (2.11)
(2.11) теңдеуінен істен шығуға дейінгі орташа пайдаланым геометриялық тұрғыдан P(t) қисығының астындағы ауданға тең (сурет 2.2). Істен шығуға дейінгі пайдаланымның статистикалық анықматамасы:
 ; (2.12)
; (2.12)
Т көрсеткіші бірінші кезекте үлкен санды элементтері бар күрделі жүйе үшін маңызды.
Істен шығуға дейінгі пайдаланымның дисперсиясы мен орташа квадраттық ауытқуы:




Қарастырлған көрсеткіштер жүйені құруда да, оны пайдалануда да (эксплуатацияда) қолданылады.
Таңдалған әдістің көмегімен жүйенің құрылымдық жүйесінен туындай отырып, оның көрсеткіштерін оларға қызмет көрсету үдерістері мен элементтерінің сипаттамаларымен байланыстыратын талдау үлгісін (моделін) анықтайды.
Құрылымдық сызба элементтерінің сенімділік сипаттамаларын таңдау бірқатар факторлармен анықталынатын қиындықтармен ұштастырылады. Олардың қатарына сенімділік көрсеткіштерінің өндірістің әр түрлі түрлерінде айрықшалануы мүмкін экплуатация жағдайларына тәуелделігі жатады, сондықтан сенімділік бойынша паспорттық мәліметтер олардың нақты мәндерімен сәйкес келмеуі мүмкін.
Қалпына келтірілмейтін жүйелер элементтерінің сенімділік көрсеткіштерін қолдана отырып, алынған математикалық үлгілер бойынша қолданбалы бағдарламалардың сәйкесінше пакеттерін қолдана отырып орындалатын сенімділік көрсеткіштерінің есебін жүзеге асырады.
15.(Показатели долговечности)Ұзақ мерзімділік -Төзімділік көрсеткіштері Ұзақ мерзімділік көрсеткішін анықтау барысында іске қосылу басталғаннан шектік қалыпқа жеткенге дейінгі ұзақтық кезедйсоқ шама болатын фактіні ескеру керек. Шектік қалып деп нәтиже соңында өнімді қолдануға келмейтін және мүмкін емес жағдайды айтады. Ұзақ мерзімділік көрсеткіші ретінде кездейсоқ шаманың орташа мәні немесе квантиль қолданылады – іске қосылу басталғаннан кейін шектік қалыпқа жеткенге дейінгі уақыт ұзақтығы. Қызмет көрсетуде ұзақ мерзімділік ресурс деп аталады, күнтізбелік уақыт бойынша – қызмет көрсету мерзімі деп аталады. Осылайша, ұзақ мерзімділік, орташа ресурсты, қызмет етудің орташа мерзімін, сонымен қатар, гамма-процентік ресурсты және гамма-проценттік қызмет көрсету мерзімін сипаттауы мүмкін. Сенімділіктің сандық көрсеткіштерін қарастырғандағы нәтижелер 1-кестеде келтірілген. Жинақы дайындық коэфиценті - бұл жұмыс басталғандағы келтірілген моментте істен шықпай жұмыс істеу ықтималдығы. Беріктік көрсеткіштері. Қолданысқа түсу ұзақтығы шектеулі шекараға дейін жүйенің жұмыс атқару уақыты деп аталады. Қызмет көрсету мерзімі Тс белгіленеді кездейсоқ айнымалы болуы мүмкін. Содан кейін ұзақ көрсеткіш ретінде орташа қызмет ету мерзімін қабылдай алады
tc=M[Tc] (4.6) немесе гамма - беріледі мерзімді пайыздық tγ қызметі Р{Tc> tγ,} = γ/100. (4.7) Осыдан, tγ, - күнтізбелік уақыт аралығы қолданысқа шыққаннан кейін, осы аралықта ол шектік жағдайына жетпейді.
Бұл көрсеткішті γ = 100%, tγ ретінде түсіндіруге болады. Беріктік көрсеткіші тек қана жұмыс уақытына тәуелді емес, эксплуатации уақытынан шектік жағдайына дейін. Сенімділіктін кешенді көрсеткіштері. Сенімділік компоненттерінің бірін сипаттайды, олардың әрқайсысы қалпына келтiрiлетiн жүйелерінің сенімділік мынадай көрсеткіштермен, сонымен қатар бірлесіп сенімділігі мен жөндеуге жарамды, кешенді көрсеткіштерін пайдаланылады. Оларға мыналар жатады: дайындық коэффиценті - kг, жедел дайындық коэффициенті - kо.г(t) және техникалық пайдалану коэффициенті - kт.и..
16.Дайындық функциясы Кд(t) жүйені t уақыт мезетінде жұмысқа қабілетті күйде табу ықтималдығын анықтаса, онда:

мұндағы j және z – жүйенің жұмысқа қабілетті және қабілетсіз күйлері. Қателік функциясы:

Дайындық коэффициентін kд анықтау үшін бірнеше әдістер қолданылуы мүмкін. Солардың біреуі t→∞ кездегі  шегін тікелей есептеуге негізделген. Екіншісі шектік теоремасын қолданады, яғни теоремаға сәйкес
шегін тікелей есептеуге негізделген. Екіншісі шектік теоремасын қолданады, яғни теоремаға сәйкес  , мұндағы р - Лапаластың айнымалы түрлендіруі;
, мұндағы р - Лапаластың айнымалы түрлендіруі;  -
-  функциясының Лаплас бойынша бейнесі. Дайындық коэффициентін дифференциалды теңдеулер жүйесін нөлге теңестіру жолымен есептеуге болады, яғни dPi (t)/ dt = 0 және алгебралық теңдеулер жүйесінің шешімі жүйенің барлық жұмысқа қабілетті күйлеріне қатысты. Осылайша, (8.9) жүйе үшін kГ-ін есептеудің алгебралық теңдеуі мына түрде болады: -λ *Po + μ *P1 =0; Po + P1=1; осыданkд = Po= μ/(μ + λ)
функциясының Лаплас бойынша бейнесі. Дайындық коэффициентін дифференциалды теңдеулер жүйесін нөлге теңестіру жолымен есептеуге болады, яғни dPi (t)/ dt = 0 және алгебралық теңдеулер жүйесінің шешімі жүйенің барлық жұмысқа қабілетті күйлеріне қатысты. Осылайша, (8.9) жүйе үшін kГ-ін есептеудің алгебралық теңдеуі мына түрде болады: -λ *Po + μ *P1 =0; Po + P1=1; осыданkд = Po= μ/(μ + λ)
Байқап отырғанымыздай, үздіксіз жүйенің дискретті уақытты жүйелер үшін дайындық коэффициентінің аналогы - бұл (8.9) алгебралық теңдеулер жүйесінен анықталатын, жүйені жұмысқа қабілетті күйде табудың шектік ықтималдығы болып табылады.
Date: 2016-05-24; view: 2634; Нарушение авторских прав