Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Фигура не является криволинейной трапецией, так как не ограничена осью абсцисс
|
|
1) 
; 
при 
(Рис. 1.);
- площадь криволинейной трапеции, ограниченной функцией 
на отрезке 
оси абсцисс: 
;
- площадь криволинейной трапеции, ограниченной функцией 
на отрезке оси абсцисс: 
;
.
2) 
; 
при (Рис. 2.);
- площадь фигуры, ограниченной функцией 
на отрезке оси абсцисс: 
;
- площадь фигуры, ограниченной функцией 
на отрезке оси абсцисс: 
;
.
3) ; при (Рис. 3.);
- площадь криволинейной трапеции, ограниченной функцией на отрезке оси абсцисс: ;
- площадь фигуры, ограниченной кривой на отрезке оси абсцисс: ;
.
Вывод: Площадь фигуры, ограниченной функциями 
и 
, удовлетворяющими условию 
при рассматриваемых значениях аргумента , вычисляется по формуле 
.
Пример: Вычислить площадь фигуры, ограниченной функциями 
и 
.
Решение:
; 
- ветви направлены вниз;
; 
; 
; 
;
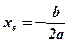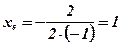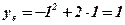- вершина параболы;
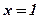- ось симметрии параболы;
| х | |||
| у | - 3 |
| х | ||
| у | - 3 |
Фигура не является криволинейной трапецией, так как не ограничена осью абсцисс. Площадь фигуры, ограниченной функциями 
и 
, удовлетворяющими условию при рассматриваемых значениях аргумента , вычисляется по формуле .
; 
.
Концы интервала, на котором построена данная фигура, являются абсциссами точек пересечения параболы и прямой .
Решим способом подстановки систему уравнений:
Û 
Û 
; 
; 
; 
.
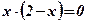Ответ: 
Замечание:
- Если плоская фигура имеет «сложную» форму, то прямыми, параллельными оси ординат, её следует разбить на части так, чтобы можно было применить уже известные формулы.
- Если фигура расположена симметрично относительно оси ординат или начала координат, то можно упростить вычисления, определив половину площади и затем удвоив результат.
Упражнения:
- Вычислить площадь фигуры, заключённой между параболой
и прямой 
. - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
. - Вычислить площадь фигуры, ограниченной функциями:
, 
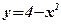. - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
, . - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
, . - Вычислить площадь фигуры, ограниченной функциями:
, , 
, . - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
, . - Вычислить площадь фигуры, ограниченной функциями:
, 
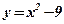. - Вычислить площадь фигуры, ограниченной функциями:
, 
. - Вычислить площадь фигуры, ограниченной функциями:
, 
. - Вычислить площадь фигуры, ограниченной функциями:
, 
.
Приложение
Date: 2016-05-13; view: 1095; Нарушение авторских прав