Критерии монодисперсности полимерных микросфер

Монодисперсным распределением полимерных частиц по размерам является такое распределение, при котором диаметр по меньшей мере 90% частиц находится в пределах 5% отклонения от среднего размера [8].

Однако, используемый в литературе термин «монодисперсность» является не точным, и критериями распределения частиц по размерам (диаметрам) являются коэффициент вариации (CV) и степень полидисперсности (PDI) [1].

Коэффициент вариации (CV) – это мера дисперсности образца, и определяется как отношение s (стандартное отклонение, которое характеризует широту распределения частиц по размерам) к (среднечисловому диаметру):

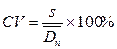(1)

(2)

При CV < 10% полимерные микросферы считаются монодисперсными.

Степень полидисперсности (PDI) – мера распределения частиц по размерам образца, которая определяется как отношение средневесового диаметра () к среднечисловому диаметру ():

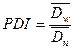(3)

При PDI = 1 – идеально монодисперсный образец.

Существует уравнение (1), которое связывает коэффициент вариации и степень полидисперсности (при условии, что распределение частиц по размерам приближено к распределению Гаусса (нормальное распределение)):

(4)

При маленьких значениях CV (<0,3, или <30%) множителем 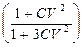можно пренебречь, и тогда .

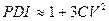Это уравнение может быть выражено кривой, приведенной на рис.1.1.1, с помощью которой можно найти значение CV, зная значение PDI, и наоборот.

Рис.1.1.1 Кривая, характеризующая отношение коэффициента вариации (CV) и степени полидисперсности (PDI).

Графически распределение частиц по размерам образца может быть представлено в виде гистограммы (дифференциальная функция распределения) – рис.1.1.2 и кумулятивной кривой (интегральная функция распределения) – рис.1.1.3.

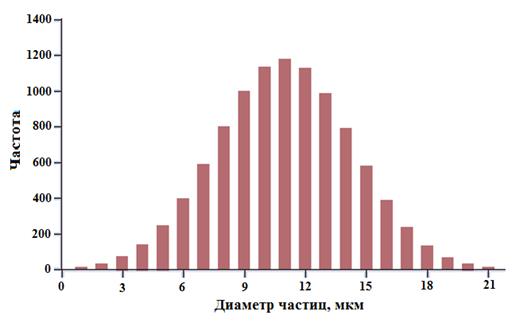
Рис.1.1.2 Гистограмма распределения частиц по размерам образца.

Рис.1.1.3 Кумулятивная кривая распределения частиц по размерам образца