
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кванттық механика негіздері
|
|
Микробөлшектердің қозғалыс заңдылықтарын зерттейтін физиканың бөлімін кванттық механика деп атайды.
Элементар бөлшектерді және осы бөлшектердің аз санынан тұратын денелерді микробөлшектер деп атаймыз. Француз ғалымы де Бройль жарықтың екі жақтылық қасиеті электронға да орындалады деген болжам ұсынды, яғни электронның механикалық қозғалысына толқындық қасиет сәйкес келеді және бұл толқынның ұзындығы келесі формуламен анықталады:
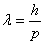 немесе
немесе 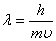 ,
,
мұндағы: р - дене импульсы,  -Планк тұрақтысы.
-Планк тұрақтысы.
Бұл өрнек де Бройль формуласы деп аталады.
Ал бөлшектің кинетикалық энергиясы 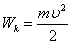 екенін ескерсек, онда де Бройльдің толқын ұзындығы кинетикалық энергия арқылы келесі түрде өрнектеледі:
екенін ескерсек, онда де Бройльдің толқын ұзындығы кинетикалық энергия арқылы келесі түрде өрнектеледі:
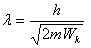 .
.
Потенциалдар айырмасы 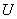 -ға тең үдетуші электр өрісінен өткен электронның энергиясы:
-ға тең үдетуші электр өрісінен өткен электронның энергиясы:
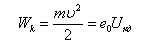
Соңғы өрнекті ескере отырып де Бройль формуласын келесі түрде өрнектеуге болады:
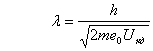 ,
,
мұндағы: 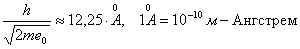 .
.
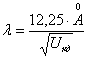 .
.
Американ ғалымы Томсон жұқа металл фольгалардан шапшаң электрондарды өткізгенде экранда дифракциялық көрініс бақылады.

Бұл дифракциялық көрініс Брэгг-Вульф шартымен сипатталады:
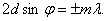
Кванттық механикада кез-келген микробөлшектің қозғалысына толқындық қозғалыс сәйкес келеді және бұл толқындық қозғалыс сол бөлшектің де Бройльдық толқын ұзындығымен сипатталады.
де Бройль толқынының амплитудасының квадраты микробөлшектің кеңістіктің берілген нүктесінде болу ықтималдығын анықтайды. Микробөлшектің кеңістіктің берілген нүктеде болу ықтималдығын анықтау үшін кеңістік пен уақыттың функциясы толқындық функция енгізілген.
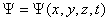 функциясы толқындық функция немесе пси функция деп аталады.
функциясы толқындық функция немесе пси функция деп аталады.
Пси функциясының модулінің квадраты микробөлшектің кеңістіктің берілген нүктесінде болу ықтималдығын анықтайды.
Толқындық функция келесі шартты қанағаттандыруы қажет:
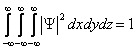 .
.
Бұл шарт нормалану шарты деп аталады.
Өзара байланысқан шамаларды анықтаудағы қателіктердің көбейтіндісі Планк тұрақтысынан кіші болмайды.
Кез-келген А және В байланысқан шамалары үшінГейзенбергтің анықталмаушылық принципі келесі түрде жазылады:
 .
.
Координата мен импульс үшін Гейзенбергтің анықталмаушылық принципі.
Координата мен импульсті анықтаудағы қателіктердің көбейтіндісі Планк тұрақтысынан кіші болмайды, яғни
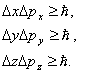
Энергия мен уақыт үшін Гейзенбергтің анықталмаушылық принципі:
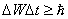 ,
,
мұндағы: 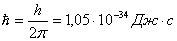 -Планк тұрақтысы.
-Планк тұрақтысы.
Date: 2016-05-18; view: 2129; Нарушение авторских прав