Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Физический смысл теоремы Гаусса
|
|
для векторов 
и 
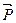
Найдем поток вектора 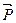через замкнутую поверхность (она обозначена пунктирной линией на рис.3.5). На основании выражения (3.11), которое справедливо для любого диэлектрика, получим
,
 |
где учтено, что вектор
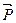равен нулю вне диэлектрика и поэтому интеграл берется по части поверхности S, расположенной внутри диэлектрика, на этой части поверхности угол между векторам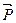и и 
равен 1800; 
– связанный заряд внутри замкнутой поверхности S (рис.3.5).
Можно показать, что полученный результат справедлив и в общем случае. Из формулы (3.12) следует, что источником вектора 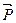являются связанные заряды. В этом и заключается физический смысл теоремы Гаусса для вектора .
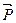. (3.12)
Для вектора электрической индукции в соответствии с формулами (3.7) и (3.11) запишем:
,
где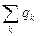 
- сумма сторонних зарядов, находящихся внутри поверхности S
. (3.13)
Формула (3.13) выражает теорему Гаусса для вектора : поток электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности сторонних зарядов. Следовательно, источником поля вектора являются свободные заряды.
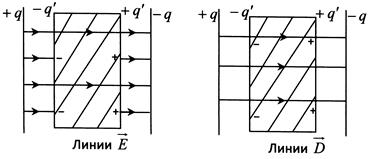а) б)
Рис.3.6. Графическое изображение поля внутри поляризованного диэлектрика
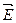с помощью линий вектора  (а) и с помощью линий вектора (б)
|
Расчет электрического поля существенно упрощается, если ввести вектор 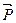, обусловленный распределением связанных зарядов (3.12), и вектор , связанный с распределением свободных зарядов q (3.13). Тот факт, что источником поля вектора являются только свободные заряды, проводит к тому, что линии на границе диэлектрика, где появляются связанные заряды , не прерываются. Это удобно для графического изображения электрического поля в присутствии диэлектрика. На рис.3.6 в качестве примера приведено графическое изображение с помощью линий 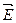и линий электрического поля плоского конденсатора, внутри которого находится прямоугольная пластина из диэлектрика с относительной диэлектрической проницаемостью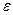 
.
Выведем формулы, связывающие свободные заряды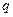 
и их поверхностную плотность 
на пластинах конденсатора со связанными зарядами и их поверхностной плотностью 
на диэлектрике. Для этого запишем для модуля напряженности 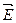электрического поля внутри пластины (см.рис.3.6,а) в соответствии с выражениями (3.2) и (3.3):
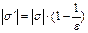; (3.14)
. (3.15)
В формуле (3.15) не выделены явно знаки зарядов 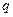и , они могут быть как больше, так и меньше нуля. Но если 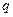>0, то тогда <0, и наоборот (это соответствует факту ослабления внешнего поля внутри диэлектрика).
Выражение (3.15) используется для выяснения физического смысла теоремы Гаусса для вектора 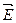электростатического поля: источником вектора 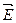являются свободные и связанные заряды. Поэтому часть линий 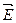на границе диэлектрика прерывается и может изменять свое направление.
Из двух векторов 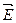и , описывающих электростатическое поле, вектор 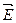является истинным вектором этого поля, так как источником 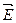являются все существующие в природе электрические заряды, а вектор – вспомогательный вектор, служащий для упрощения расчета электрического поля в присутствии диэлектрика.
Date: 2016-05-18; view: 1231; Нарушение авторских прав