Энергия системы зарядов

Получим выражение для потенциальной энергии системы двух точечных зарядов и , находящихся на расстоянии 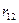. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют, и энергия в этом случае равна нулю. При сближении зарядов на расстояние 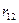совершается работа против сил электрического поля, которая идет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая к или к .Работа переноса заряда из бесконечности в точку, удаленную от на 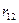, равна

,

где - потенциал, создаваемый зарядом в той точке, в которую перемещается заряд . Аналогично работа переноса заряда из бесконечности в точку, удаленную от на , равна

,

где - потенциал, создаваемый зарядом в той точке, в которую перемещается заряд .

Значение работ в обоих случаях одинаково и каждое из них выражает энергию системы:

.

Для того чтобы в выражение энергии системы оба заряда входили симметрично, запишем его следующим образом:

. (5.1)

Формула (5.1) задает энергию системы двух зарядов. Перенесем из бесконечности еще один заряд и поместим его в точку, находящуюся на расстоянии от и от . При этом совершается работа

,

где - потенциал, создаваемый зарядами и в той точке, в которую перемещается заряд .

В сумме с и 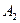работа 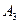будет равна энергии трех зарядов:

. (5.2)

Выражение (5.2) можно привести к виду:

Добавляя к системе зарядов последовательно и т.д., можно убедиться в том, что в случае N зарядов потенциальная энергия системы равна:

, (5.3)

где - потенциал, создаваемый в той точке, где находится , всеми зарядами, кроме k-го.

Date: 2016-05-18; view: 487; Нарушение авторских прав