Магнитное поле прямого тока

Пусть постоянный ток течет вдоль бесконечно длинного прямого провода, имеющего круглое сечение радиусом . Найти индукцию поля снаружи и внутри провода.

Линии вектора имеют вид окружностей с центром на оси провода. Причем модуль вектора должен быть одинаков во всех точках на расстоянии 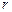от оси провода. Поэтому по теореме о циркуляции вектора для круглого контура (рис. 1.11, а) , следовательно, вне провода

, (). (1.13)

Решение этой задачи с помощью закона Био–Савара–Лапласа оказывается гораздо более сложным.

Из соображений симметрии следует, что линии вектора внутри провода являются тоже окружностями. По теореме о циркуляции вектора для круглого контура (рис. 1.11, а) , где 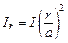– ток, охватываемый данным контуром. Отсюда находим, что внутри провода

, .

Зависимость показана на рис. 1.11, б.

Если провод имеет вид трубки, то снаружи индукция определяется формулой (1.13), а внутри – магнитное поле отсутствует. Это также легко показать с помощью теоремы о циркуляции вектора .

Date: 2016-05-18; view: 380; Нарушение авторских прав