Движение заряженных частиц в магнитном поле

Считаем, что магнитное поле однородно и на частицы не действуют электрические поля. Рассмотрим три возможных случая.

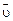1. – заряженная частица движется в магнитном поле вдоль линий магнитной индукции (угол между векторами и равен или ). Сила Лоренца равна нулю. Магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

2. – заряженная частица движется в магнитном поле перпендикулярно линиям магнитной индукции (). Сила Лоренца постоянна по модулю и перпендикулярна вектору скорости. Частица будет двигаться по окружности радиусом с центростремительным ускорением . Из второго закона Ньютона получаем радиус окружности и период вращения .

3. Заряженная частица движется под углом к линиям магнитной индукции. Тогда движение частицы можно представить в виде суммы двух движений (рис. 1.8):

а) равномерного прямолинейного движения вдоль поля со скоростью ;

б) равномерного движения по окружности в плоскости, перпендикулярной полю, со скоростью .

Суммарное движение будет движением по спирали, ось которой параллельна магнитному полю. Шаг винтовой линии , где 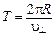– период вращения частицы, и . Тогда

.

Если магнитное поле неоднородно и заряженная частица движется под углом к линиям магнитного поля в направлении возрастания поля, то величины и уменьшаются с ростом . На этом основана фокусировка заряженных частиц магнитным полем.

Магнитный поток

Рассмотрим плоскую площадку , находящуюся в однородном магнитном поле с индукцией . Магнитным потоком или потоком вектора магнитной индукции сквозь площадку называют величину

,

где – угол между направлением нормали 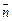к площадке и направлением индукции ; – проекция вектора на нормаль .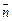

Магнитный поток – скалярная знакопеременная величина. Если угол острый, то поток положительный, если угол тупой, то поток отрицательный, при поток равен нулю.

Поскольку – число линий магнитной индукции, проходящих через единицу поверхности рассматриваемой площадки, то магнитный поток равен полному числу линий магнитной индукции, проходящих через данную поверхность.

Если магнитное поле неоднородно, а рассматриваемая поверхность не плоская, то эту поверхность можно разбить на бесконечно малые элементы 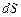. Каждый элемент поверхности можно рассматривать как плоскую площадку, а любое поле на протяжении этого элемента – как однородное. Поэтому магнитный поток через элемент поверхности

,

а полный поток через всю поверхность

.

В единицах СИ поток измеряется в веберах (Вб).

1.11. Работа, совершаемая при перемещении проводника
с током в магнитном поле

Сила 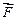, действующая на перемычку

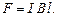
При перемещении из положения 1 в положение 2 на расстояние перемычка под действием силы совершит работу , где – заштрихованная площадь, – поток вектора магнитной индукции, пронизывающий эту площадь.

В итоге получим:

,

т.е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива и для произвольного направления вектора .

Date: 2016-05-18; view: 511; Нарушение авторских прав