
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определенный интеграл как предел интегральной суммы
|
|
Содержание
| Введение ……………………………………………………………….. | |
| Справочный материал…………………………………………………. | |
| Задания расчетно-графической работы...……………………………. | |
| Решение варианта № 0 ……………………………………………… | |
| Ответы …………………………………………………………………. | |
| Список рекомендуемой литературы …………………………………. | |
Введение
Математика соединяет в себе полярно противоположные элементы – логику и интуицию, анализ и конструкцию, общность и конкретность, совместное действие и синтез которых обеспечивает высокую ценность математической науки. Колоссальное прикладное значение имеют дифференциальное и интегральное исчисления.
Предлагаемая расчетно-графическая работа содержит 30 вариантов, в каждом из которых по восемь заданий, охватывающих основные вопросы темы «Определенный интеграл». Указанные задачи предназначены для повторения и закрепления изученного материала, а также для самостоятельной работы студентов, которая является важнейшим условием для усвоения теоретического и практического курса.
Предлагаемые методические указания включают справочный материал и основные формулы, относящиеся к данному разделу математики, а также подробное решение аналогичных задач нулевого варианта. В конце приведены ответы к каждому заданию всех вариантов.
СПРАВОЧНЫЙ МАТЕРИАЛ
Определенный интеграл как предел интегральной суммы.
Пусть у = f(x) – непрерывная функция на [a;b], (a<b). Выполним следующие действия:
1. Разобьем отрезок точками x0 = a < x1 < … < xn = b на n частичных отрезков [x0;x1], [x1;x2],…,[x n-1; x n ].
2. В каждом частичном отрезке [x i-1;x i ] выберем произвольную точку  и вычислим значение функции в ней
и вычислим значение функции в ней  .
.
3. Составим сумму  . Сумма такого вида называется интегральной суммой функции y = f(x) на отрезке [a;b].
. Сумма такого вида называется интегральной суммой функции y = f(x) на отрезке [a;b].
4. Обозначим через  – длину наибольшего частичного отрезка.
– длину наибольшего частичного отрезка.
5. Найдем предел интегральной суммы, когда n→∞, т.е.  :
:
 .
.
Если существует конечный предел интегральной суммы при  и он не зависит ни от способа разбиения на элементарные части, ни от выбора
и он не зависит ни от способа разбиения на элементарные части, ни от выбора  , то этот предел называется определенным интегралом функции f(x) на отрезке [a;b] и обозначается
, то этот предел называется определенным интегралом функции f(x) на отрезке [a;b] и обозначается  .
.
Свойства определенного интеграла.
10.  .
.
20. 
 .
.
30. 
40. Свойство аддитивности определенного интеграла:

50. Если  [a;b]
[a;b]  , то
, то  .
.
70. Если 
 [a;b], то
[a;b], то 
80. Теорема об оценке определенного интеграла.
Пусть функция у=f(x) непрерывна на [a;b],  ;
;  , тогда
, тогда 
90. Теорема о среднем
Пусть функция у=f(x) непрерывна на [a;b], тогда существует хотя бы одна точка 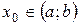 такая, что
такая, что  .
.
Теорема. Формула Ньютона – Лейбница.
Пусть f(x) – непрерывна на [a;b]; F(x) – некоторая ее первообразная на [a;b], тогда 
Date: 2016-05-18; view: 358; Нарушение авторских прав