Вопрос № 18. Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом. Уравнение пучка прямых

На плоскости дана точка 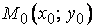. Прямая, угловой коэффициент которой задан, проходит через эту точку 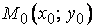(рис. 6). Уравнение ее имеет вид:

Рис. 6. Уравнение прямой, проходящей через заданную точку 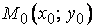, с заданным угловым коэффициентом k

Всякое уравнение первой степени относительно декартовых координат изображает прямую линию, и обратно, всякая прямая линия изображается в декартовых координатах уравнением первой степени.

Уравнение прямой, разрешенное относительно ординаты , имеет вид:

(1)

Параметр k характеризует направление прямой и называется ее угловым коэффициентом. В случае прямоугольной системы координаты: 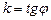, где - угол, образованный прямой с положительным направлением оси абсцисс. В случай косоугольной системы координат: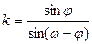

Второй параметр уравнения (1), свободный член b, равен величине отрезка, отсекаемого данной прямой на оси ординат, считая от начала координат.

Если известны угловые коэффициенты 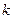и двух прямых, то угол 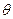между этими прямыми вычисляется для прямоугольной системы координат и по формуле: 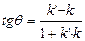, для косоугольной системы:

Условие параллельности двух прямых выразится так:

Условие перпендикулярности двух прямых:

Для прямоугольной системы и для косоугольной системы координат:

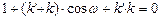. Прямая, проходящая через точку (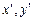) и имеющая угловой коэффициент 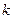, изображается уравнением:

Нормальное уравнение прямой имеет следующий вид: при 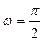, или в общем виде: , обозначает длин перпендикуляра, опущенного из начала координат на данную прямую (); обозначает угол между этим перпендикуляром и положительным направлением оси 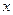; - угол между этим же перпендикуляром и осью :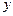

Всякое уравнение первой степени 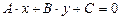может быть приведено к нормальному виду, для чего достаточно умножить его на нормирующий множитель: при 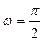, в общем случай: . Нормирующий множитель должен иметь знак, обратный знаку свободного члена данного уравнения. Если 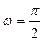, то параметры соответствующей прямой вычисляются по формулам: 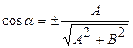, , , в случае косоугольной системы координаты: ,

, .

Date: 2016-05-18; view: 1292; Нарушение авторских прав