Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вопрос № 7. Способы вычисления определителей второго и третьего порядка
|
|
Определитель второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка след образом:
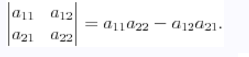
Определитель третьего порядка,, называется число, которое вычисляется по формуле:
Способы вычисления определителей второго порядка:
А) Чтобы вычислить определитель матрицы 
второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
Способы вычисления определителей третьего порядка:
А) Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком "плюс"; аналогично, для второго определителя - соответствующие произведения берутся со знаком "минус", т.е.
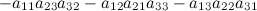
Б) Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":
Date: 2016-05-18; view: 486; Нарушение авторских прав