Зависимость между силой и скоростью сокращения мышц

Исторически сложилось так, что вначале была изучена зависимость скорости сокращения мышцы от величины нагрузки при преодолевающем (концентрическом) режиме и только затем – при уступающем (эксцентрическом).

В. Фенн и Б. Марч (W.O. Fenn, B.S. March, 1935) проводили эксперименты на изолированных мышцах лягушки и кошки. Они первыми предложили для описания зависимости «сила-скорость» укорочения мышцы эмпирическую формулу (1.3):

F= F₀e^-aV-kV (1.3),

где: F – сила мышцы; F₀ – максимальная сила, развиваемая мышцей при V=0 (изометрический режим сокращения); V – скорость сокращения мышцы; а,k – эмпирические константы (рис. 1.3).

Рис. 1.3. Зависимость скорости укорочения мышцы от нагрузки при одиночном сокращении m.sartorius лягушки, 144 мг, t = 18,5 Co

В последующем М. Полиссар (M.J. Polissar, 1952) и Х. Обер (X. Aubert, 1956) предложили другие формулы (1.4, 1.5), основанные на экспоненциальной и логарифмической зависимостях.

F= F₀e^{-FV/ bF}₀-Va/b (M.J. Polissar, 1952) (1.4), где: a,b – константы;

V = B ln (A/P+F)) (X. Aubert, 1956) (1.5),

где: А, В – константы, P – масса груза, F – небольшая внутренняя «фрикционная сила», противодействующая укорочению. Формулы (1.4 и 1.5) имеют хорошее соответствие экспериментальным данным (B.R. Jewell, D.R. Wilkie, 1960).

Несмотря на хорошее соответствие экспериментальных результатов и формул М. Полиссара и Х. Обера, широкую популярность приобрело уравнение Хилла (A. Hill, 1938), опубликованное тремя годами позже В. Фенна и Б. Марча. Это объясняется тем, что А. Хиллу удалось установить две фундаментальные закономерности, присущие мышечному сокращению. Изучая теплопродукцию мышцы, он обратил внимание на поразительный факт: при любой скорости сокращения и любых нагрузках количество теплоты, выделяемое мышцей, зависит только от изменения длины мышцы. Кроме того, он обнаружил, что при одинаковом изменении длины мышцы скорость выхода на новый изометрический уровень уменьшалась с увеличением нагрузки. Таким образом, А. Хилл получил соотношение между скоростью сокращения мышцы и внешней нагрузкой (1.6).

V = b (P₀- P)/ (P+a) (1.6),

где: P_o – максимальная масса груза, при котором не происходит укорочения мышцы; Р – масса груза; a, b – константы.

Вид зависимости «сила-скорость» различен для быстрых и медленных мышц Дж. Уэллс (J.B. Wells, 1965) показал, что быстрая мышца (m.tibialis anterior) способна показать значительно более высокие значения силы при той же скорости укорочения по сравнению с медленной мышцей (m.soleus). Это означает, что мощность, развиваемая быстрой мышцей, будет в 2-3 раза выше, чем у медленной мышцы.

Исследования зависимости «сила-скорость» на мышцах человека начались с середины двадцатого века (R.J. Dern, J.M. Leven, H.A. Blair, 1947; H.J. Ralston et al., 1949; D.R. Wilkie, 1950) и затем были активно продолжены (P.V. Komi, 1973; E. Pertuson, S. Bouisset, 1973). Специально сконструированные динамометры позволяли задавать различную величину внешней нагрузки и регистрировать угол между плечом и предплечьем, тангенциальное ускорение, электрическую активность мышц-сгибателей и разгибателей предплечья. Посредством создания математической модели движения руки определялись усилия, развиваемые мышцами, длина и скорость их сокращения. Показано, что полученные результаты хорошо согласуются с уравнением Хилла (рис. 1.4). Последующие исследования (A. Thorstensson, G. Grimby, J. Karlsson, 1976; V. Eloranta, P.V. Komi, 1980) показали, что для мышц нижних конечностей человека основная закономерность (уменьшение силы мышцы с ростом скорости укорочения) сохраняется.

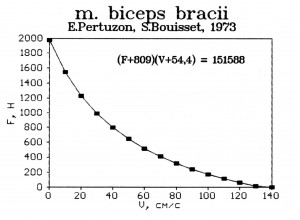
Рис. 1.4. Зависимость «сила – скорость» для m.biceps brachii человека (по: E. Pertuson, S. Bouisset, 1973)

Следует отметить, что изучение зависимости «сила-скорость» (концентрический режим) привлекало внимание многих исследователей, в то время как эксцентрический режим оставался менее исследованным. А. Хилл (A. Hill, 1951) находил, что при эксцентрическом режиме сокращения мышцы сила, проявляемая ею, растет. P.V. Komi (1973) использовал специальный динамометр для регистрации усилий, развиваемых m.biceps brachii человека в концентрическом и эксцентрическом режимах сокращения мышцы. Полученные результаты свидетельствуют о том (рис. 1.5), что при работе m. biceps brachii в концентрическом режиме зависимость «сила-скорость» может быть описана уравнением гиперболы.

Рис. 1.5. Зависимость между силой и скоростью сокращения m. biceps brachii человека (по: P.V. Komi, 1973)

Рис. 1.6. Зависимость «сила – скорость сокращения» мышц нижней конечности человека при ходьбе в гору (по: J.B. Morrison, 1970)

При эксцентрическом режиме сокращения увеличение скорости растяжения мышцы приводит к увеличению силы, развиваемой мышцей. Результаты Дж. Моррисона (J.B. Morrison, 1970) показывают (рис. 1.6), что с ростом скорости раст h4 style="text-align: justify;"/pp style="text-align: justify;" яжени/td laquo;сила-длинаp style="text-align: justify;"/supя мышцы увеличение проявля‐/p емой ею силы наблюдается только у m.rectus femoris. У остальных мышц при увеличении скорости растяжения сила, проявляемая ими, очень быстро уменьшается до нуля.

Date: 2016-05-17; view: 1676; Нарушение авторских прав