Среднее линейное и квадратическое отклонение

Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

Дисперсия

Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия простая:

В нашем примере:

Дисперсия взвешенная:

Более удобно вычислять дисперсию по формуле:

Вопрос 17 -правило сложения дисперсий

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

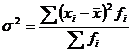
Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:

где - среднее значение результативного признака по i-ой группе;

- общая средняя по совокупности в целом;

- объем (численность) i-ой группы.

Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основание группировки.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

где - дисперсия результативного признака в i-ой группе;

- объем (численность) i-ой группы;

Date: 2016-05-16; view: 409; Нарушение авторских прав