
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Затухающие электрические колебания
|
|

Каждый реальный колебательный контур обладает активным сопротивлением, и энергия, запасённая в контуре, постепенно расходуется на нагревание и излучение. Свободные колебания будут затухающими. Выражение закона Ома, написанное для цепи 1-3-2, изображенной на рис.18, имеет вид:
 (69)
(69)
Разделив это уравнение на  и учтя,
и учтя,  , получим:
, получим:
 . (70)
. (70)
Приняв во внимание, что 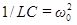 , и введя обозначение
, и введя обозначение  , уравнению (70) можно придать следующий вид:
, уравнению (70) можно придать следующий вид:
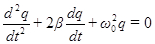 . (71)
. (71)
Последнее уравнение совпадает с дифференциальным уравнением затухающих колебаний (32).
При условии, что  решение уравнения (71) имеет вид:
решение уравнения (71) имеет вид:
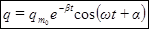 , (72)
, (72)
где
 . (73)
. (73)
Таким образом, частота затухающих колебаний  меньше собственной частоты
меньше собственной частоты  .
.
Величину  называют периодом затухающих колебаний, несмотря на то, что функция (72) не периодическая.
называют периодом затухающих колебаний, несмотря на то, что функция (72) не периодическая.
 , (74)
, (74)
где  - период свободных незатухающих колебаний. Период затухающих колебаний больше периода собственных незатухающих колебаний. Зная зависимость
- период свободных незатухающих колебаний. Период затухающих колебаний больше периода собственных незатухающих колебаний. Зная зависимость  можно найти напряжение на конденсаторе и ток в контуре:
можно найти напряжение на конденсаторе и ток в контуре:
 (75)
(75)
 .
.
Умножив правую часть этой формулы на равное единице выражение  , получим
, получим
 .
.
Введя угол 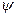 , определяемый условиями
, определяемый условиями
 ,
,  ,
,
можно написать
 . (76).
. (76).
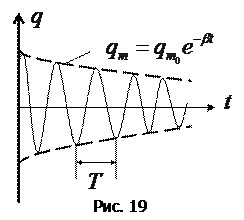 Поскольку
Поскольку  а
а  значение
значение 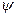 заключено в пределах
заключено в пределах  до
до  . Таким образом, при наличии в контуре активного сопротивления сила тока опережает по фазе напряжение на конденсаторе более чем на
. Таким образом, при наличии в контуре активного сопротивления сила тока опережает по фазе напряжение на конденсаторе более чем на  (при
(при  опережение составляет
опережение составляет  ).
).
График функции (72) изображен на рис.19. Графики для напряжения и силы тока имеют аналогичный вид.
Затухание колебаний характеризуется рядом величин, рассмотренных нами при анализе затухающих механических колебаний (коэффициент затухания  , время релаксации
, время релаксации  , логарифмический декремент затухания
, логарифмический декремент затухания  , добротность
, добротность  ). Если затухание мало (
). Если затухание мало (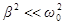 ), то
), то  и. тогда
и. тогда
 , (77)
, (77)
 . (78)
. (78)
Есть ещё одна полезная формула для добротности в случае слабого затухания:
 . (79)
. (79)
где  – энергия, запасенная в контуре,
– энергия, запасенная в контуре,  – уменьшение этой энергии за период
– уменьшение этой энергии за период  .
.
В самом деле, энергия пропорциональна квадрату амплитуды заряда конденсатора, т.е.  . Отсюда относительное уменьшение энергии за период
. Отсюда относительное уменьшение энергии за период  . Учитывая, что
. Учитывая, что  , получаем формулу (79).
, получаем формулу (79).
В заключение отметим, что при  вместо колебаний будет происходить апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называется критическим:
вместо колебаний будет происходить апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называется критическим:


 . (80)
. (80)
Date: 2016-05-15; view: 368; Нарушение авторских прав