Принцип суперпозиции. Интерференция волн

Принцип суперпозиции (наложения) волн: при распространении в среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы каждой волны.

Интерференция волн – наложение двух (или нескольких) когерентных волн, в результате чего происходит усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн.

Когерентными называются волны одного направления одинаковой частоты и постоянной разности фаз.

Рассмотрим наложение двух когерентных волн, возбуждаемых точечными источниками (для простоты начальные фазы ):

.

Разность фаз этих колебаний равна

, (115)

где - разность хода волн, - длина волны.

1) если колебания происходят в одинаковой фазе, т.е. 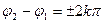(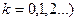, (116)

то наблюдается максимум интерференции. Приравниваем (115) и (116):

.

Получаем условие максимума при интерференции:

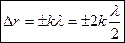(. (117)

В этом случае .

2) если колебания происходят в противофазе, т.е.

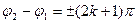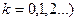(, (118)

то наблюдается минимум интерференции. Приравниваем (115) и (117):

.

Получаем условие минимума при интерференции:

(. (118)

В этом случае .

Стоячие волны

Особым случаем интерференции являются стоячие волны – это волны, образующиеся при наложении двух волн одинаковой частоты и амплитуды, распространяющихся навстречу друг другу.

Такой случай можно реализовать, заставив бегущую волну отразиться от преграды (рис. 24).

Уравнения падающей и отражённой волн имеют вид:

.

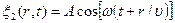Сложив эти уравнения, используя тригонометрические преобразования, получаем уравнение стоячей волны:

, (119)

где амплитуда стоячей волны:

. (120)

Из выражения (120) видно, что амплитуда стоячей волны

. (121)

Точки, в которых амплитуды бегущей и отражённой волны складываются, называются пучностями ().

Точки, в которых амплитуда равна нулю, называются узлами (). Эти точки колебаний не совершают.

Пучность образуется в тех точках, где колебания бегущей и отражённой волн происходят в одинаковой фазе, т.е. (). Следовательно, координаты пучностей:

(). (122)

Узлы образуются там, где колебания происходят в противофазах, т.е. (). Следовательно, координаты узлов:

(). (123)

Длиной стоячей волны называется расстояние между пучностями или узлами: .

Таким образом, длина стоячей волны равна половине длины складываемых волн:

. (124)

Стоячая волна не переносит энергии, т.к. энергия переносится в равных количествах бегущей и отражённой волнами.

Date: 2016-05-15; view: 407; Нарушение авторских прав