Сложение взаимно перпендикулярных колебаний

Допустим, что материальная точка (тело) может совершать колебания как вдоль оси , так и вдоль перпендикулярной оси 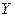. Если возбудить оба колебания, материальная точка будет двигаться по некоторой криволинейной траектории, форма которой зависит от разности фаз колебаний. Выберем начало отсчета времени так, чтобы начальная фаза одного колебания была равна нулю. Тогда уравнения запишутся следующим образом:

, (22)

где - разность фаз складываемых колебаний, и 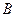— амплитуды колебаний.

Выражения (22) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (22) параметр . Из первого уравнения следует, что

, (23)

следовательно,

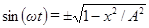(24).

Теперь развернем косинус во втором уравнении из (22) по формуле для косинуса суммы ( и подставим в него вместо и их значения (23) и (24). В результате получим:

.

Перенесем все члены без корня в левую часть уравнения и возведем его в квадрат. После несложных преобразований получим уравнение эллипса, оси которого повернуты относительно координатных осей:

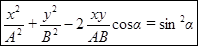(25)

Ориентация эллипса и величина полуосей зависят довольно сложным образом от амплитуд и 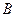и разности фаз .

Рассмотрим некоторые частные случаи.

1. Разность фаз .

В этом случае уравнение (25) примет вид , откуда получается уравнение прямой:

(26).

Результирующее движение является гармоническим с частотой и амплитудой (рис 8).

2. Разность фаз . В этом случае уравнение (25) примет вид ,

откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис.9):

. (27)

3. Разность фаз .

Уравнение (25) переходит в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний (рис.10):

. (28)

При равенстве амплитуд и 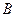эллипс вырождается в окружность. Случаи и отличаются направлением движения по эллипсу или по окружности.

Если , уравнения (22) можно записать следующим образом: .

В момент тело находится в точке (рис 10). В последующие моменты времени, координата уменьшается, а координата становится отрицательной. Следовательно, движение совершается по часовой стрелке.

Если , уравнения колебаний имеют вид:

.

Отсюда можно заключить, что движение происходит против часовой стрелки.

Из сказанного следует, что равномерное движение по окружности радиусом с угловой скоростью может быть представлено как сумма двух взаимно перпендикулярных колебаний:

. (29)

(знак «+» в выражении для соответствует движению против часовой стрелки, знак «-» – по часовой стрелке).

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину , их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз. В самом деле, уравнения колебаний можно представить следующим образом:

где выражение рассматривается как разность фаз, медленно изменяющуюся со временем по линейному закону.

Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от до .

Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу.

На рис.11 показана одна из простейших траекторий, получающаяся при отношении частот 1:2 и разности фаз . Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу.

Фигуры Лиссажу позволяют найти частоту одного из колебаний, если известна частота другого. Это обусловлено тем, что кратность частот легко находится с помощью секущих, параллельных координатным осям.

Date: 2016-05-15; view: 619; Нарушение авторских прав