Методические указания к выполнению задания. 1. Определить приближенные значения отрезка Ох, в котором может быть решение данной системы

1. Определить приближенные значения отрезка Ох, в котором может быть решение данной системы. Возьмем отрезок [0;1]. (Отрезок выбирать исходя из области допустимых значений х).

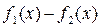
2. 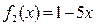Протабулировать функции и в этом отрезке (см. рис.17).

3. Для всех значений аргумента х вычислить.

4. Построить графики функций по полученным табличным значениям.

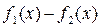Из графика следует, что функции в отрезке [0;1] имеют общую точку, т.е. пересекаются, но разность далека от заданной точности e=0,0001.

Рис.17. Решение системы 2-х нелинейных уравнений (пример 5.4.1.)

5. 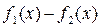Уточнить решение:

- задать значения а=0,6, b=0,7 (в концах этого отрезка разность принимает значения разных знаков);

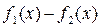- обратить внимание на изменения в графиках и табличные значения;

- наименьшая разность = -0,03;

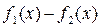- полученная точность не удовлетворяет заданной, потому задаем новые значения a=0,65; b=0,66 (рис.17).

- в этом отрезке достигается необходимая точность: = 0,0001

- решение системы в отрезке [0,65;0,66]: х=0,65330, у=-2,6660 получено за два шага уточнений (итераций).

6. 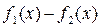Выполнить проверку подбором параметра (Сервис † Подбор параметра, см.5.3)

- подобрать =0 для х;

- вычислить y как y =f₁(x) или y =f₂(x).

5.4.2. Варианты заданий по теме:

«Решение системы 2-х нелинейных уравнений»

Решить систему нелинейных уравнений с заданной точностью e = 0,001. Выполнить проверку с помощью итераций.

№	задание	№	задание	№	задание

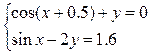
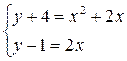
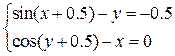
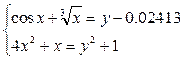
6. Лабораторная работа по теме: «Массивы»

Цель работы: изучение матричных операций и операций с векторами в Excel, реализуемых с помощью формул массива.

Теоретическая справка. Формулы массива называют также табличными форму­лами. Формулы массива — очень мощное средство Excel, позволяющее в форму­лах обращаться с блоком ячеек, как с единым целым. Такие формулы позволяют давать компактные решения сложных задач.

Массивы можно использовать для создания формул, которые возвращают некоторое множество результатов или оперируют множеством значений, а не отдельными значениями.

Формула массива использует

несколько множеств значений,

называемых массивами аргументов,

и возвращает одно или несколько

значений.

Правила применения формулы массива:

1) выделить ячейку или диапазон, который будет содержать результаты (диапазон такого же размера и формы, что и диапазон с исходными данными);

2) ввести формулу вычисления выражения, содержащего массивы аргументов;

3) нажать Ctrl + Shift + Enter для фиксации ввода формулы массива Excel заключает формулу в фигурные скобки (признак формулы массива).

G Примечания.

1. Редактировать отдельные ячейки массива нельзя. Ячейки в диапазоне массива рассматриваются как единое целое, и редактировать их надо все сразу.

2. Для изменения или очистки массива следует выделить весь массив и активизировать строку формул. (Фигурные скобки вокруг формулы исчезнут.) Изменить или очистить формулу и нажать Ctrl + Shift + Enter.

Date: 2016-05-13; view: 411; Нарушение авторских прав