Дисперсионный анализ: проверка различий для нескольких выборок

Дисперсионный анализ (сокращенно ANOVA) дает общую схему проверки статистических гипотез, основанную на тщательном изучении различных источников вариации (изменчивости, неоднородности) в сложной ситуации. Ниже приведены некоторые примеры ситуаций, в которых следует использовать дисперсионный анализ.

Ситуация первая. С целью сокращения расходов вы проанализировали пять добавок, которые, предположительно, увеличивают объём продукции химического производства. Вы десять раз запускали процесс производства с использованием каждой из добавок и десять раз без добавки. Это пример однофакторной модели, так как имеется один фактор ("добавка"), который имеет несколько значений (уровней). Результат представляет собой набор данных, состоящий из 6 списков значений объема продукции. Из-за обычной изменчивости, свойственной процессу, трудно объяснить, обусловлено ли любое улучшение просто случайной удачей, или данная добавка действительно лучше других. Поэтому необходимо проверить нулевую гипотезу: действительно ли эти шесть списков значений объемов продукции одинаковы и все различия между ними являются результатом только лишь случайности. Использовать для проверки t- тест, рассмотренный нами ранее, нельзя, поскольку речь идет более, чем о двух выборках. Вы можете использовать t-тест для независимых выборок, чтобы сравнивать добавки попарно. Однако ввиду необходимости 15-и таких проверок эта группа тестов не является обоснованной, поскольку мы не управляем вероятностью ошибки для группы. В частности, если принять истинность нулевой гипотезы о том, что различия в объемах продукции нет, то вероятность сделать неверное утверждение о том, что некоторые пары объемов продукции значимо различаются, может быть намного выше, чем ошибка в 5%, которую применяют для каждого отдельного теста. Использование F-теста позволяетудержать ошибку на уровне 5%, и затем, если F-тест оказывается значимым, можно использовать модифицированные t-тесты. Вместо попарного t-теста применяют однофакторный дисперсионный анализ, призванный выяснить, есть ли какие-либо значимые (т.е. систематические, неслучайные) различия между этими добавками. Если значимые различия имеются, то можно продолжить их подробное изучение. В противном случае можно сделать вывод, что фиксируемых систематических различий между добавками нет.

Ситуация вторая. В принципе, можно использовать в производственном процессе комбинацию добавок. При наличии 5 добавок возможно 2⁵ = 32 комбинации (включая и отсутствие добавок), причем для каждой комбинации технологический процесс необходимо запустить дважды. Имеет смысл использовать каждую комбинацию более одного раза, если есть такая возможность, потому что это позволяет получить больше информации об изменчивости в каждой ситуации. Этот пример представляет собой факторный план с пятью факторами (добавками), каждая из которых изучается на двух уровнях (либо используется, либо не используется). Дисперсионный анализ такого набора данных покажет, (а) влияет ли каждая добавка на объем продукции и (б) существует ли взаимодействие влияний добавок в комбинации.

Ситуация третья. Как часть маркетингового исследования, вы проверили три вида средств массовой информации (газету, радио и телевидение) в сочетании с двумя типами рекламного объявления (прямой, и косвенный методы). Каждому испытуемому в этом исследовании была продемонстрирована одна комбинация, после чего был подсчитан результат (в баллах), отражающий эффективность рекламы. Это пример двухфакторного плана (факторами являются "вид средства массовой информации" и "тип рекламного объявления"). Дисперсионный анализ покажет, (а) существенно ли различаются виды средств массовой информации по эффективности и (б) существует ли взаимосвязь между видом средства массовой информации и типом рекламного объявления.

Для проверки каждой гипотезы в дисперсионном анализе используют F-тест, основанный на F-статистике, которая представляет собой отношение двух дисперсий. (Вспомним, что дисперсия представляет собой квадрат стандартного отклонения и именно этот показатель изменчивости используют в дисперсионном анализе). Числитель представляет собой вариацию, обусловленную конкретным интересующим нас эффектом, который мы и проверяем, а знаменатель — вариацию, обусловленную случайностью. Если это отношение больше табличного F- значения, то фактор имеет значимое влияние.

Однофакторный дисперсионный анализ, в частности, используют для проверки значимости различия средних значений нескольких различных выборок. Это самый простой вид дисперсионного анализа. Хотя более сложные ситуации требуют более сложных вычислений, общий подход остается тем же: проверить значимость, сравнив один источник вариации (проверяемый фактор) с другим источником вариации (лежащим в основе случайности).

Пример. Сравнение качества продукции поставщиков.

F – тест определяет, значимо ли различаются средние

F – тест в однофакторном дисперсионном анализе устанавливает, значимо ли различаются средние нескольких независимых выборок. Он заменяет t-тест для независимых выборок при наличии более двух выборок и дает тот же результат в случае двух выборок.

Данные и источники вариации

Набор данных в однофакторном дисперсионном анализе состоит из k независимых выборок, элементы которых измерены в одинаковых единицах (например, рубли, километры). Допустимы различные размеры выборок. Форма данных показана в табл. 15.2.1.

Таблица15.2.1.Данные для однофакторного дисперсионного анализа

	Выборка1	Выборка2	………….	Выборка k
	X1,1 X1,2 …. …. X1,n1	X2,1 X2,2 …. …. X2,n2	…. …. …. …. ….	Xk,1 Xk,2 …. …. Xk,nk
Среднее			….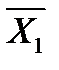
Стандартное отклонение	S1	S2	….	Sk
Размер выборки	n1	n2	….	nk

Чтобы определить источник вариации, следует ответить на вопрос: “Почему значения данных отличаются друг от друга?” Поскольку здесь два источника вариации, значит, и два ответа на этот вопрос.

1. Одним из источников вариации является факт отличия друг от друга генеральных совокупностей. Например, если выборка 2 включает особенно тщательную обработку, то значения в выборке 2 будут отличаться (будут выше) от значений в других выборках. Этот источник называется межгрупповая (межвыборочная) вариация. Чем больше межгрупповая вариация, тем очевиднее, что генеральные совокупности различаются между собой.

2. Другим источником вариации является (обычно) неоднородность значений внутри каждой выборки. Например, вы не можете ожидать, что все значения в выборке 2 будут одинаковыми. Этот источник называют внутригрупповой (внутривыборочной) вариацией. Чем больше внутригрупповая вариация, тем случайнее ваши данные и тем труднее установить, действительно ли различаются генеральные совокупности.

Источники вариации в однофакторном дисперсионном анализе

· Межгрупповая вариация (между выборками).

· Внутригрупповая вариация (внутри каждой выборки).

В примере с поставщиками двумя источниками вариации являются (1) возможно различные уровни качества трех поставщиков и (2) возможно различные опенки качества различных компонентов, полученных от одного поставщика. F-тест будет основан иа отношении величин этих источников вариации. Но сначала рассмотрим основные положения проверки этой гипотезы.

Date: 2016-05-14; view: 859; Нарушение авторских прав